Zbadać istnienie ekstremów lokalnych funkcji kuba: Zbadać istnienie ekstremów lokalnych funkcji, gdy: f(x)= 1/3 x³− 1/2x²−12x+5

Qulka: f' = x²−x−12 =0 delta x1 x2 i tam są ekstrema lokalne

Janek191:

	1		1
f(x) =		x3 −		x2 −12 x + 5
	3		2

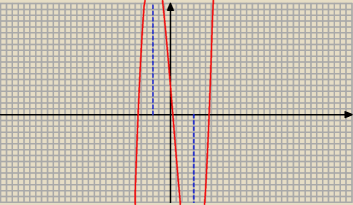
więc f '(x) = x² − x −12 = 0 ⇔ ( x − 4)*( x + 3) = 0 ⇔ x = − 3 lub x = 4 W punkcie x = − 3 pochodna f ' zmienia znak z + na − , więc f osiąga maksimum lokalne y_max = f( − 3) = − 9 − 4,5 + 36 + 5 = 27,5 W punkcie x = 4 pochodna zmienia znak z − na + , więc f osiąga minimum

	64		2
lokalne ymin = f(4) =		− 8 − 48 + 5 = − 29
	3		3