Geomatria analityczna licealna- trudne Razor3: Na prostej 3x−2y+5=0 wyznacz współrzędne punktu P takiego, by suma odległości AP i PB była najmniejsza dla A(4,2) i B(5,−1). Jak się zabrać za to zadanie?

5-latek: O tej godzinie to spac

Razor3: Jeszcze wczesna pora!

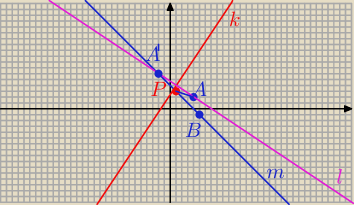
PW: To proste. Sprawdzasz, że A i B leżą po jednej stronie prostej k (rachunkowo). Wyznaczasz punkt A' będący obrazem A w symetrii o osi k. Stwierdzasz, że |AP| + |PB| = |A'P| + |PB|. Suma odległości |A'P| + |PB| jest najmniejsza, gdy P leży między A' i B. P jest zatem częścią wspólną prostyej k i prostej A'B.

Janek191: 3 x − 2 y + 5 = 0 to y = 1,5 x + 2,5 P = ( x ; 1,5 x + 2,5) bo leży na danej prostej A = ( 4 , 2) B = ( 5, − 1)

	2
y = −		x + b
	3

	2
2 = −		*4 + b
	3

	8		14
b = 2 +		=
	3		3

	2		14
l : y = −		x +
	3		3

A ' punkt symetryczny do A

	2		14
1,5 x + 2,5 = −		x+		/ * 6
	3		3

9 x + 15 = − 4 x + 28 13 x = 13 x = 1 −−− y = 1,5*1 + 2,5 = 4 −−−−−−−−−−−−−−−−− S = ( 1 ; 4) A ' = ( x' , y' ) Mamy

x' + 4		y ' + 2
	= 1		= 4
2		2

x' = − 2 y' = 6 A ' = ( − 2 , 6 ) =========== m − prosta A' B B = ( 5; − 1) 6 = − 2a + b₁ − 1 = 5 a + b₁ −−−−−−−−−−− 7 = − 7 a a = − 1 b₁ = 6 + 2*(−1) = 4 y = − x + 4 ======== zatem y = 1,5 x + 2,5 y = − x + 4 −−−−−−−−−− 1,5 x + 2,5 = − x + 4 / * 2 3 x + 5 = − 2 x + 8 5 x = 3

	3
x =		= 0,6
	5

y = −0,6 + 4 = 3,4 P = ( 0,6 ; 3,4) ============

Janek191: Rozwiązanie według propozycji PW:

Razor3: Wielkie dzięki! Tylko nie rozumiem dlaczego "Suma odległości |A'P| + |PB| jest najmniejsza, gdy P leży między A' i B."?

Janek191:: Z prawa Δ

Razor3: A dokładniej?

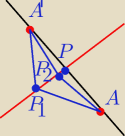
Janek191::

PW: Dokładniej: jest to aksjomat geometrii euklidesowej zwany potocznie nierównością trójkąta. Mówi on, że dla dowolnych trzech punktów płaszczyzny |AB| < |AC| + |CB| z wyjątkiem przypadku, gdy punkt C leży między A i B, wtedy |AC|+|CB| = |AB|. "Leżenie między" to relacja uporządkowania punktów na prostej, wyrażona w postaci innego aksjomatu. Wystarczy ją rozumieć intuicyjnie.

Razor3: Racja! Intuicyjnie to do mnie przemawia(bo tak jest, bo innego przypadku nie ma), ale do końca nie rozumiem.