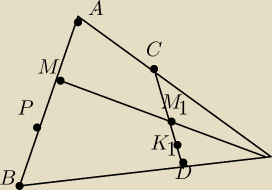
Zadanie nr 7 funkcja 5-latek: Zadanie nr 7 : X jest zbiorem punktow odcinka AB , Y−zbiorem punktow odcinka CD . Punktowi M odcinka AB (M∊X ) przyporzadkowujemy punkt M₁ (jak na rysunku Znajdz obrazy punktow A B i P w tym przyporzadkowaniu . czy jest ono funkcja odzworowujaca zbior X na zbior Y ? Co jest obrazem odcinka AP ? Znajdz przeciwobraz punktu K₁ Czy nasz rysunek okresla jaks funkcje odwzorowujaca zbior Y na zbior X Czy ta ostatnia funkcja przypomina CI cos fizycznego ? Tu sie poddaje

5-latek: Chociaz tak zapiszmy X={A, M, P, B} Y={C, M₁, K₁,D} Obrazy punktow A, B,P f((A))=C f((B))=D f((P))= K₁ (ale tu nie jestem pewien

5-latek: Chociaz tez sie zastana wiam nad tym czy f((P))=∅

5-latek: Spojrzy ktos?

5-latek: Podbiję

Eve: jesli P i K₁ są współliniowe z wysokością, to masz dobrze f(P jesli n ie to f(P)=∅

Eve: jednokładność, jeśli CD II AB

5-latek: napiszse CI tak na rysunku w ksiazce odleglosc punktu P od punktu B= 1cm Natomiast odleglosc punktu K₁ od punktu D= 0,8cm

5-latek: Eve troche jeszce materialu do jednokladnosci

Eve: poczekaj, na razie nic nie widzę

5-latek: Dobrze. To sa poczatki funkcji (1 klasa liceum

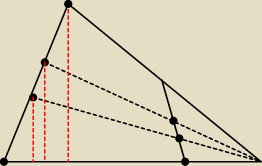
Eve: przychodzi mi do głowy tylko pole trójkąta

Eve: ale to ni jak ma się do argumentów i wartości

5-latek: Do tego zadania mam tylko taka odpowiedz Przypomina cien od punktowego zrodla światla Ale jesli f((p))=K₁ to moze dalej czy jest ono funkcja odwzorowujaca zbior X na Y ?(tak Co jest obrazem odcinka AP? to f((AP))= CK₁ Znajdz przeciwobraz punktu K₁ to f⁻¹((K₁))= P czy nasz rysunek okresla jakas funkcje odwzorowujaca zbior Y na X ? (nie wiem

5-latek: To pewnie bedzie proste ( a my mamy nadmiar wiadomosci Moze pojawi sie Mila (ona ma ta ksiazke lub Gray .

Eve: no nie mam pojęcia i dziwne to, ten cień światła punktowego

5-latek: Eve nie ma cisnienia na to zadanie

Saizou : może analogicznie jak się udowadnia równoliczność dwóch odcinków

5-latek: Czesc A mialbys jakis pomysl na to zadanie ?

Gray: Z czym dokładnie macie problem? Przecież to jest zwykła funkcja przekształcająca jeden odcinek w (a dokładniej "na") drugi. Jest to przekształcenie wzajemnie jednoznaczne.

5-latek: Witaj Moze po kolei czy dobrze mam wyznaczone obrazy punktow A, B, P ? czy dobrze mam wyznaczony obraz odcinka AP ? czy dobrze tez mam wyznaczony przeciwobraz K₁ ? Potem wrocimy do przeksztalcenia wzajemnie jednoznacznego Dobrze?

5-latek: Gray Powrocimy moze do tego jutro . Ja juz muszse isc spac bo jutro rano do pracy Jesli bedziesz jutro na forum to poprosze Cie o powrot do tego zadania . Dobrze?

Gray: Dobrze. Miłych snów.

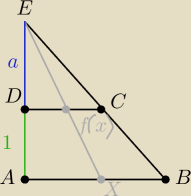
Saizou : Bez strat dla ogólności mogę przyjąć że D<C oraz A<B oraz że C−D<B−A zatem

B−A		C−D		f(x)−D		X−A
	=		oraz		=
1+a		a		a		a+1

wówczas

a		C−D
	=
1+a		B−A

	X−A		a		C−D
f(x)=		*a+D=		(X−A)+D=		(X−A)+D
	a+1		a+1		B−A

a funkcja f(x) jest różnowartościowa i "na"

5-latek: Dzieki ale wydaje mi sie ze chyba za bardzo matematycznie podchodzisz do tego

5-latek: Chociaz moze tak ma byc

Gray: No jestem.

5-latek: No to jeszcze raz witaj Moze najpierw obrazy punktow A,B,P Obrazem punktu A jest punkt C Obrazem punktu B jest D natomiast obraz punktu P (nie za bardzo wiem czy punkt K₁

5-latek: Dobrze na razie ?

Saizou : tak, zobacz na moją funkcję którą napisałem

	C−D
f(A)=		(A−A)+D=D
	B−A

	C−D
f(B)=		(B−A)+D=C−D+D=C
	B−A

5-latek: Dobrze. jesli tak to jest ono funkcja roznowartosciowa i na bo odwzorowanie to przyjmuj swoje wartosci tylko raz i kazdy element zbioru Y jest wartoscia dla kazdego elementu zbioru X Takze wobec tego obrazem odcinka AP jest odcinek CK₁ To przeciwobraz K₁ co bedzie ?

Saizou : no to będzie P

5-latek: To czyli tak jak napisalem wczoraj o 19:19 Teraz tak . Jestto odwzorowanie roznowartosciowe i odwzorowanie na (zbior X na zbior Y ) czyli wzjajemnie jednoznaczne Natomiast odzwzorowanie u nas Yna X jest funkcja odwotna do odwzorowania X na Y

Saizou : no tak mi się wydaje

5-latek: OK? Moze jak pojawi sie Gray to sprawdzi albo moze jutro poprosze jeszcze Mile

5-latek: Nie chce jej dzisiaj meczyc

Gray: Sprawdziłem − wszystko OK.

5-latek: Dziekuje CI

zombi: Swoją drogą wskazując tę funkcję pokazaliście, że dwa odcinki domknięte są ze sobą równoliczne. Saizou wspomniał o tym.

Gray: Jedna rzecz: jeżeli chodzi o uzasadnienie, to ja nie zrozumiałem tego co Saizou napisał.

	C−D
Takie rozpisanie na funkcję i ilorazy typu		mogę nie przejść. No bo na dobrą sprawę
	B−A

jak rozumieć dzielenie przez B−A, jeżeli B i A to punkty z R² (czy aby na pewno z R²?)? I co to znaczy, że A<B? Jak rozumiem, nie mamy tu żadnego układu współrzędnych (to zadanie z planimetrii, a nie z geometrii analitycznej)...