Ekstrema, Monotoniczność - sprawdzenie. noname1: Proszę o pomoc (sprawdzenie) − ekstrema, monotoniczność: Mam taką funkcję: f(x)=x√4−x² 1. Dziedzina funkcji wyszła mi od <−2,2>

	2x2
2. pochodna z tej funkcji y'=(x√4−x2)'=√4−x2−
	2√4−x2

3. Część wspólna dziedziny z funkcji głównej i pochodnej wyszła mi: (−2,2) 4. Po przyrównaniu wyniku z pochodnej do 0, otrzymałem

	2x2
√4−x2−		/*2√4−x2
	2√4−x2

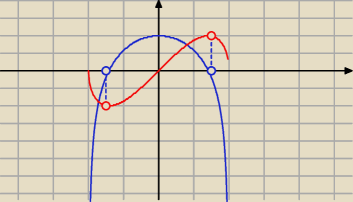
2√4−x²−2x²=0 /:2 (√4−x²)²−x²=0 x=2 i x=−2 oraz x=0 Wykres narysowany od dołu odbija się w "2" przechodzi przez 0 i odbija się w "−2" i z wykresu wyszło f rośnie dla x ∊ (−2,0) i f maleje dla x∊(0,2) a f(max) = (0,0) Może ktoś sprawdzić?

noname1: Pomoże ktoś?

Tadeusz: źle policzyłeś to f'(x)=0

noname1: jak powinno wyjsc? albo gdzie robie blad?

Dziadek Mróz: f(x) = x√4 − x² 1. D: 4 − x² ≥ 0 x² ≤ 4 x ≤ ±2 x = 0 D = {x ∊ ℛ : −2 ≤ x ≤ 2} 2. y = x√4 − x² y = uv u = x v = √z z = 4 − x² y' = [uv]' = u'v + uv' = *) u' = [x]' = 1

	1
v' = [√z]' =		* z' = **)
	2√z

z' = [4 − x²]' = −2x

	x
**) = −
	√4 − x2

	x2		2(x2 − 2)
*) = √4 − x2 −		= −
	√4 − x2		√4 − x2

4. y' = 0

	2(x2 − 2)
−		= 0
	√4 − x2

D: √4 − x² ≠ 0 4 − x² > 0 x < ±2 2(x² − 2) = 0 x² − 2 = 0 x² = 2 x = ±√2

noname1: Dzięki

noname1: a może mi ktoś napisać jeszcze jak wyszło to przejście z :

	x2		2(x2−2)
√4−x2−		=
	√4−x2		√4−x2

Rozumiem, ze sprowadzic do wspolnego mianownika, ale nie wiem jak dojsc do tej postaci. Mogłby ktos rozpisac to przejscie?

noname1: Dobra juz wiem. Udalo mi sie