FUNKCJE WYKŁADNICZE I LOGARYTMICZNE Zdzisiu: 1.Funkcja f dana jest wzorem f(x)=a^x−2+p. Wyznacz a i p, jeżeli do jej wykresu należą punkty a(3, p+2) oraz B (2log₂4,1). Tutaj policzyłem, że 2log₂4 = 4, więc punkt B(4,1). I dalej nie wiem co z tym zrobić 2.Wykres funkcji f(x)=(2^x−1−8)/4 jest symetryczny względem osi OX do wykresu funkcji g. Zapisz wzór funkcji g i naszkicuj jej wykres. Dla jakich argumentów funkcja g przyjmuje wartości dodatnie? Prosiłbym o pomoc, jak rozwiązać te zadania. Pozdrawiam

Tadeusz: podstawiaj współrzędne tych punktów do równania funkcji p+2=a³⁻²+p ⇒ a= ... 1=a⁴⁻²+p ⇒ p= ...

Zdzisiu: No tak, wyszło mi, sam powinienem na to wpaść, dzięki a drugie wiesz?

Tadeusz:

	2x−1−8
f(x)=
	4

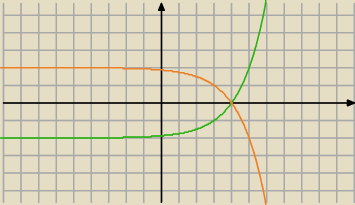
f(x)=2^x−3−2 i krzywa zielona g(x)=−f(x)=2−2^x−3 i krzywa ruda −

Zdzisiu: a mógłbyś mi jeszcze wytłumaczyć jak przekształciłeś f(x)?

Zdzisiu: f(x)={2^x−1−2³}{4}

Zdzisiu:

	2x−1−23
f(x)=
	4

Zdzisiu:

	2x−1−23
f(x)=
	4

Zdzisiu: już wiem

Tadeusz: −