| 6 | ||
f(x) = | ||
| |x−2| |
| 2x−|x+1| | ||
f(x) = | ||
| x−1 |
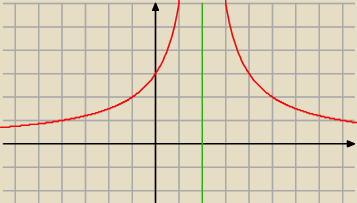Proszse to wykres 1 funkcji Mozesz zobaczyc
mógłbyś mi wytłumaczyc ? gubie sie przy funkcjach z wartością
bezwzględną...
No to proszse
| 6 | ||
f(x)= | ||
| |x−2| |
| 6 | ||
Wiec nasza funkcja dla xnalezy (2,oo) bedzie miala postac f(x)= | ||
| x−2 |
| 6 | ||
Wiec doa x nalezy (−oo,2) nasza funkcja bedzie miala postac f(x)= | ||
| 2−x |
bardzo dziękuje za wytłumaczenie 
! 
a tu moje obliczenia:
D= R\{1}
|x+1|=0, czyli x=−1 −> nie ma sensu
| 2x−x+1 | x+1 | |||
x>−1 więc (−1; ∞) i funkcja przybiera postac | czyli | dla tego | ||
| x−1 | x−1 |
| 2x−(−x−1) | 3x−1 | |||
x<−1 więc (−∞; −1) i funkcja przyjmuje postac | czyli | dla tego | ||
| x−1 | x−1 |
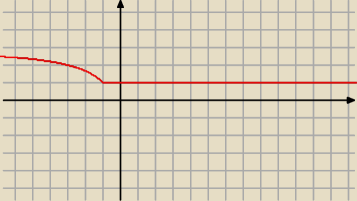To jest wykres tej drugiej funkcji
Tutaj jest troche inaczej bo wartosc bezwzgledna jest w liczniku a niew mianowniku wiec |x+1|=0
dla x=−1
wiec dla x≥−1 (to zgodnie z definicja wartosci bezwzglednej bedzie ≥ a nie > |x+1|=x+1 wiec
| 2x−(x+1) | x−1 | |||
dla tego przedzialu funkcja bedzie miala postac f(x)= | = | =1 (czyli | ||
| x−1 | x−1 |
| 2x−(−x−1) | 2x+x+1 | |||
znakiem nasza funkcja bedzie miala postac f(x)= | = | = | ||
| x−1 | x−1 |
| 3x+1 | 3x+1 | 3(x−1)+4 | 4 | 4 | ||||||
Teraz y= | = | = 3+ | = | +3 ( to jest | ||||||
| x−1 | x−1 | x−1 | x−1 | x−1 |
dziękuje Ci bardzo bardzo bardzo !