Funkcje trygonometryczne xyz: Wiedząc, że α i β są kątami ostrymi trójkąta prostokątnego i spełniona jest równość 4 sin² α − 5 sin² β = 1, oblicz: a) wartość funkcji sinus, cosinus i tangens kąta α, b) wartość wyrażenia sinα*cosβ + cosα*sinβ + tgα*tgβ, c) miary kątów α i β z dokładnością do 1 stopnia.

Eve: sinα=cosβ, sinβ=cosα − korzystaj jak wolisz

xyz: Niestety i tak nie wiem jak to zrobić bo rozumiem, że mam podstawić np. zamiast sinα cosβ, ale nie wiem co dalej.

xyz: Niestety i tak nie wiem jak to zrobić bo rozumiem, że mam podstawić np. zamiast sinα cosβ, ale nie wiem co dalej.

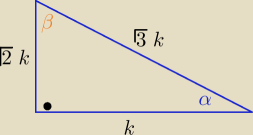
Eta: Dla kątów ostrych w trójkącie prostokątnym sin²α+cos²α=1 i sinβ= cosα , tgβ= ctgα i tgα*ctgα=1 to 4sin²α−5cos²α= sin²α+cos²α ⇒ 3sin²α= 6cos²α ⇒ tg²α=2 ⇒ tgα= √2 a= √2k, k>0 , b= k , c= √2k²+k²= √3k a) tgα= √2 , sinα=......... cosα=........ b)............ c).............. dokończ ......