Dla jakich wartości parametru k równanie (...) ma 3 rozwiązania
meqo: Dla jakich wartości parametru k równanie |x2−4| = (k2−5) |x−2| ma 3 rozwiązania, z których
jedno jest dodatnie i dwa są ujemne?
15 lut 12:37
Gray:
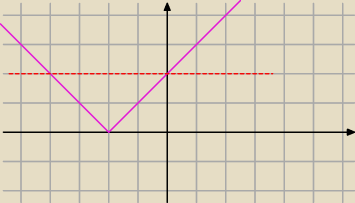
Jednym z rozwiązań jest x=2.
Dla x≠2, po podzieleniu stronami przez |x−2| otrzymujesz:
|x+2|=k
2−5.
To najłatwiej rozwiązać graficznie. Aby Twoje wyjściowe równanie miało pożądane rozwiązania,
musi być spełniony warunek 0<k
2−5<2, gdyż k
2−5 to prosta pozioma, która musi leżeć pomiędzy
osią Ox a prostą y=2 (zaznaczoną na rysunku na czerwono). Stąd wyliczasz k.
15 lut 12:56
J:
⇔ Ix−2I*Ix+2I − Ix−2I(k2−5) = 0 ⇔ Ix−2I*[Ix+2I − (k2−5)] = 0
ponieważ Ix−2I = 0 ma jedno dodatnie, więc Ix+2I − (k2−5) = 0 musi mieć dwa ujemne,
a to ma miejsce, gdy: 0 < k2 −5 < 2
15 lut 12:56
J:
Cześć
Gray ...

15 lut 12:57
Gray: Cześć
J 
15 lut 13:00
Eta:
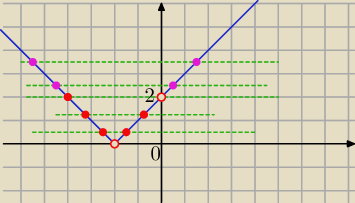
.....
dla k
2−5<0 równanie jest sprzeczne
|x−2|*|x+2|=(k
2−5)*|x−2| ⇒ |x−2|=0 lub |x+2|=k
2−5
x=2 −−− jedno dodatnie rozwiązanie
graficznie, rysujemy wykresy:
f(x)=|x+2| ,
g(x)= m , gdzie
m=k2−5
to dwa ujemne rozwiązania są dla :
m∊(0,2)
rozwiąż układ nierówności:
i podaj odp:............
15 lut 13:01
Eta:

15 lut 13:01
Eta:
Piszcie "chłopy", które następne rozwiązujecie

co bym na darmo nie pisała

15 lut 13:03
J:
wcale nie na darmo

Twoje wyjaśnienie jest bardzo obszerne

15 lut 13:05
Eta:
@
Gray "dzielimy przez |x−2|" −−−− gubimy rozwiązanie x=2

15 lut 13:12
Gray: Nic nie gubimy

2 już jest w koszyku z rozwiązaniami.
15 lut 13:31
 Jednym z rozwiązań jest x=2.
Dla x≠2, po podzieleniu stronami przez |x−2| otrzymujesz:
|x+2|=k2−5.
To najłatwiej rozwiązać graficznie. Aby Twoje wyjściowe równanie miało pożądane rozwiązania,
musi być spełniony warunek 0<k2−5<2, gdyż k2−5 to prosta pozioma, która musi leżeć pomiędzy
osią Ox a prostą y=2 (zaznaczoną na rysunku na czerwono). Stąd wyliczasz k.
Jednym z rozwiązań jest x=2.
Dla x≠2, po podzieleniu stronami przez |x−2| otrzymujesz:
|x+2|=k2−5.
To najłatwiej rozwiązać graficznie. Aby Twoje wyjściowe równanie miało pożądane rozwiązania,
musi być spełniony warunek 0<k2−5<2, gdyż k2−5 to prosta pozioma, która musi leżeć pomiędzy
osią Ox a prostą y=2 (zaznaczoną na rysunku na czerwono). Stąd wyliczasz k.


 .....
dla k2−5<0 równanie jest sprzeczne
|x−2|*|x+2|=(k2−5)*|x−2| ⇒ |x−2|=0 lub |x+2|=k2−5
x=2 −−− jedno dodatnie rozwiązanie
graficznie, rysujemy wykresy:
f(x)=|x+2| , g(x)= m , gdzie m=k2−5
to dwa ujemne rozwiązania są dla :
m∊(0,2)
rozwiąż układ nierówności:
.....
dla k2−5<0 równanie jest sprzeczne
|x−2|*|x+2|=(k2−5)*|x−2| ⇒ |x−2|=0 lub |x+2|=k2−5
x=2 −−− jedno dodatnie rozwiązanie
graficznie, rysujemy wykresy:
f(x)=|x+2| , g(x)= m , gdzie m=k2−5
to dwa ujemne rozwiązania są dla :
m∊(0,2)
rozwiąż układ nierówności:

 co bym na darmo nie pisała
co bym na darmo nie pisała 
 Twoje wyjaśnienie jest bardzo obszerne
Twoje wyjaśnienie jest bardzo obszerne 

 2 już jest w koszyku z rozwiązaniami.
2 już jest w koszyku z rozwiązaniami.