równania trygonometryczne SoS: 1−sin2x/2=1

Ada: sinx = 0

SoS: Jakieś wyjaśnienie ? Najlepiej rozpisanie po kolei ?

SoS: Dochodzę do momentu sin2x= −1 pomożecie ?

Ada: 1−1 = 0 nie mam momentu sin2x = −1

SoS: czy dobrze jest tak x= −π/4 + 2kπ v x=( π+ π/4)+2kπ , k∊C

SoS: całość jest dzielona przez 2 ( 1−sin2x)/2 =1

SoS:

1−sin2x
	=1
2

5-latek: A jaki ma byc zapis ?

	1−sin2x		sin2x
czy		=1 czy 1−		=1?
	2		2

SoS: pierwszy

SoS: 5−latek pomożesz ?

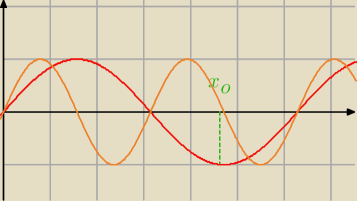
Ada: No to robi kolosalną różnicę, bo z tego co ty tam napisałeś/aś wyglądało to na: pomarańczowy sin2x czerwony sinx

	2x
1−sin		= 1
	2

Twoje: sin2x = −1

	1
x0 =		π
	2

sinus jest ujemny w III (x = x₀ + π) i IV ćwiartce (x= − x₀)

	3		−1
2x =		π + 2kπ ⋁ 2x =		π+2kπ
	2		2

	3		−1
x=		π + kπ x =		π + kπ
	4		4

Ale zauważasz, że oba wyniki są względem siebie przesunięte o pi, więc możesz jeden pominąć.

SoS: a mi wyszło ....

	−π		π
x=		+2kπ lub x= (π+		) +2kπ
	4		4

SoS: w sin nie dodajemy 2kπ

Ada: dodajemy, ale całość dzielisz przez 2 później. Przeanalizuj 3 ostatnie linijki

SoS: Tylko ja wgl inaczej robiłem sin 2x= −1 2x0= −π/2 x0=− π/4 ?

SoS: zle

Qulka: dobrze tylko nie dopisałeś okresu a jest nieskończenie wiele rozwiązań zależnie od k

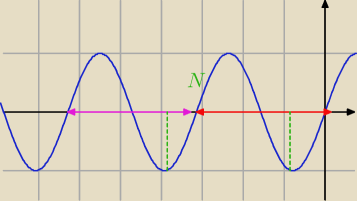
Ada: No to źle robiłeś. Przyjrzyj się wykresowi funkcji sin(2x). Rozwiązanie −1 pojawia się co okres π. Za pomocą czerwonych i różowych strzałek zaznaczone są przedziały o długości π, na zielono rozwiązania.

SoS: i zawsze musze doprowadzać do postaci x = ...... czy moge zostawic np 2x= ......

Ada: Zawsze doprowadzasz do x=... I zawsze dodajesz 2kπ (dla sinus, kosinus) lub kπ (dla tangensów i kotangensów). Dzieląc, mnożąc, etc. x przeskalowujesz funkcję w całej dziedzinie.

SoS: Dzięki wielkie już trochę się rozjaśniło ale mam problem z wartością bezwzględna I 1−√2 sin x I = 2

Ada: Jak zwykłą wartość bezwzględną, na przedziały: 1−√2 sin x = 2 lub 1−√2 sin x = −2 Dostajesz 4 rozwiązania, sprawdzasz czy nie "zachodzą" na siebie.

SoS: coś mi się nie zgadza z odp przykład 2cos(3x− π/2) = −1 ja mam x= π/18 + 2kπ/3 lub= 5/18π + 2/3kπ w odp jest x= − π/18 + 2kπ/3 lub 7/18π+2kπ/3

Ada:

	π		π		1
cos(3x−		) = cos(		− 3x) = sin(3x) = −
	2		2		2

	1
x0 =		π
	6

	7		−1
3x =		π + 2kπ lub 3x =		π + 2kπ
	6		6

SoS: a nie powinno byc − π/3

Ada:

	1		1
Nie,		π ⇔ 30o a		π ⇔ 60o
	6		3

SoS: przecież ma być cos = − 1/2 to chyba bd x0 = − π/3

Ada: widzisz przekształcenie między kosinusem, a sinusem

SoS: tak, ale mnie uczyli ze mam się kątem ,, nie przejmować, nie patrzec na niego ... "

Ada: Mi chodzi o to, że mam

	−1		1
sinus x =		⇒ x =		π
	2		6

	−1		1
a nie kosinus =		⇒ x =		π
	2		3