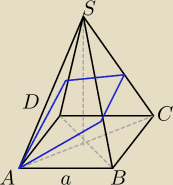
krótkie, proste zadanie ze stereometrii Michał: Witam, Mam problem z prostym zadaniem z stereometrii. Tzn. liczę na swój sposób, ale odpowiedź wychodzi mi całkowicie inna niż poprawna. Oto jego treść: Na rysunku obok przedstawiono ostrosłup prawidlowy czworokątny o wszystkich krawędziach równej długosci. Oblicz pole przekroju zaznaczonego na rysunku, jeśli płaszczyzna przekroju tworzy z podstawą kąt 30 stopni. Proszę o pomoc. Ja rozdzieliłem go na dwa oddzielne ostrosłupy, gdzie jeden jest podobny do drugiego i potem na bazie podobieństwa, policzyłem pole płaszczyzny, ale to było mnóstwo liczenia ( w dodatku chyba źle) i coś nie pykło. Domyślam się, że zauważenie czegoś znacznie uprości rozwiązanie. Pozdrawiam

wmboczek: Kąt między krawędzią boczną i podstawą to 45 możesz wyznaczyć przekątne deltoidu z tw cosinusów

Michał: Odświeżam, proszę o więcej wskazówek. Nie wiem jak zastosować rady wmboczka, bo wychodzi mi, że mam zbyt mało danych do twierdzenia cosinusów.

wmboczek: z trygonometrii policzysz wysokość od podstawy do przekroju h=a√6/6 z kąta 45 i tej wysokości wyznaczysz krótszą przekątną d₁=a√2−a√6/3 dla dłuższej przekątnej rozważ trójkąt o kątach 30,45 i 105. Narysuj jego wysokość H, która podzieli a√2 na 2 części. tg30=(a√2−2)/x gdzie x to rzut d₂ na podstawę

wmboczek: tg30=(a√2−x)/x sry coś ostatnio nieuważnie piszę

Magda: Jak policzyć długość krótszej przekątnej deltoidu? Bo nie rozumiem