oblicz a i b xxx: Wykres funkcji g(x)=^x+2_3x−3 powstał przes przesunięcie wykresu funkcji f(x)=¹_x+1 p wektor[a,b].Oblicz a i b

xxx: tam zamiast p ma byc o wektor

5-latek:

	1		1
g(x)=		+
	x−1		3

Janek191:

	x + 3
g(x) =		?
	3 x − 3

	1
f(x) =		?
	x + 1

5-latek: Wykres funkcji f(x) nalezy narysowac y=¹_x i przesunac go o [−1 0] (czyli w lewo o 1 jednostke

	1		1
natomiast g(x) nalezy narysowac wykres y=		i przesunac go wektor [1		] czyli w
	x		3

	1
prawo o 1 jednostke i do gory o		jednostki
	3

tak wiec zeby z wykresu f(x) otrzmac wykres g(x) nalezy f(x) przesunac o 2 jednostki w prawo

	1		1
i		do gowry czyli o wektor [2		]
	3		3

powinno byc dobrze

5-latek: Proszse o sprawdzenie (tez mi sie przyda

Mila:

x+2		1		x+2
	=		*		=
3*(x−1)		3		x−1

	1		x−1+3		1		3		1		1
=		*[		]=		*[1+		]=		+		postać kanoniczna g(x)
	3		x−1		3		x−1		3		x−1

	1
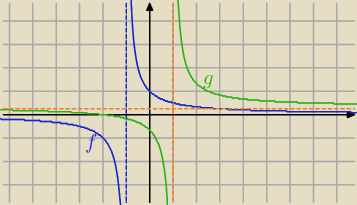
f(x)→[2,		]→g(x)
	3

	1
Asymptota pionowa przesunięta o 2 jednostki w prawo, asymptota pozioma o		j. w górę
	3

Spr.

	1		1		1
f(x−2)+		=		+		=
	3		x−2+1		3

	1		1		3+x−1		x+2
=		+		=		=		=g(x)
	x−1		3		3*(x−1)		3x−3

5-latek: Dziekuje CI bardzo za dokladne opisanie

Mila: