Okrag K: Punkt B(1,1) jest wierzchołkiem kąta prostego w trójkącie prostokątnym o polu 2, wpisanym w okrąg x2+y2+2x−2y−2=0. Znajdź współrzędne pozostałych wierzchołków tego trójkąta. Wiem, że musze znaleźć dwie proste prostopadłe przecinające sie w B. Tylo nie wiem jak. Może ktos podpowiedzieć, co po kolei powinnam zrobić?

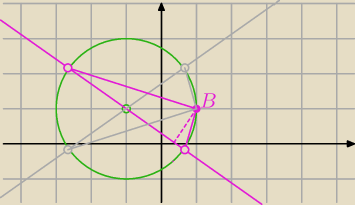
Tadeusz: Podstawa |AC| Twego trójkąta ma miarę 4 ... zatem jego wysokość musi być równa 1 (odległość B od AC) Szukamy równania prostej zawierającej podstawę AC Prostą tą zapiszemy w postaci ogólnej ale wykorzystując fakt, że przechodzi ona przez punkt 0 y−1=a(x+1) ⇒ ax−y+a+1=0

	|a−1+a+1|		√2
1=		⇒ √2=|2a| ⇒ a=±
	√1+1		2

dalej już dla Ciebie −

K: Super, dziekuje bardzo

Tadeusz: − dalej poradzisz?

K: Okay, czyli teraz prostą która mi wyszła musze podstawić do równania okregu i otrzymam punkty przecięcia. Zgadza się ?

Qulka: tak

K: mam tylko jeszcze pytanie, skąd ten wzór na prostą

K: mam tylko jeszcze pytanie, skąd ten wzór na prostą

Tadeusz: Wiesz, że proste przechodzą przez 0=(−1,1) i znasz ich współczynniki kierunkowe (proste są dwie)

Qulka: tablice maturalne strona 5

Qulka: wzór na prostą o współczynniku a przechodzącą przez P

Tadeusz: nie uczą teraz równania pęku prostych −:(