asdf asdf: z drutu o długości 100 cm zrobiono szkielet prostopadłościanu o podstawie kwadratu. Przy jakiej długości krawędzi podstawy pole powierzchni całkowitej tego prostopadłościanu ma wartość największą?

	1
mam pytanie czy w tym zadaniu wystarczyło by podzielić przez 12 i wynik by był 8		czyli
	3

taki jak w odpowiedzi i napisać ze największą powierzchnię całkowitą ma sześcian czy trzeba by było robić całe zadanie po kolei?

Eve: prostopadłościan nie ma wszystkich krawędzi równych, tak, jak założyłeś

wmboczek: Ale skąd wiemy że to sześcian? Czy potrafisz to uzasadnić? Jak tak to napisać i OK, jak nie to punty w plecy

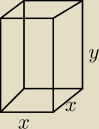
Mila: S_k=8x+4y=100 2x+y=25⇔y=25−2x, 25−2x>0⇔ P(x)=2x²+4*x*(25−2x) P(x)=2x²+100x−8x² P(x)=−6x²+100x

	−100		25
xw=		=
	−12		3

Dla x=8¹₃ funkcja kwadratowa P(x) osiąga największą wartość.