Zadanie
Aagher: Z kwadratowego arkusza blachy o boku długości 80 cm wycięto w narożach cztery przystające
kwadraty o boku długości x. Otrzymany profil odpowiednio zgięto, stykające się krawędzie
zlutowano i w ten sposób otrzymano prostopadłościenna skrzynie (bez górnego wieka) Dla jakiej
wartości x pojemność otrzymanej skrzyni jest największa ? Wyznacz tę pojemność.
Moim problemem jest to, że nie mogę sobie wyobrazić jak to mogłoby się to zgiąć.
Prosiłbym o wytłumaczenie.
13 lut 17:15
Qulka:
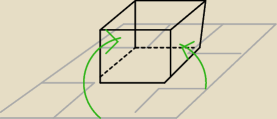
13 lut 17:19
Qulka: mogłam te odcięte przerywaną

13 lut 17:20
Mila:
Prosta sprawa, robisz model, to jak zabawa dla przedszkolaka.
13 lut 17:48
Aagher: V=(80−2x)2 *x
13 lut 17:50
Mila:
Dobrze.
x∊(0,40)
Teraz licz pochodną i jej miejsce zerowe.
13 lut 18:01
Mila:
Może licz w decymetrach, będą prostsze rachunki.
V(x)=(8−2x)2*x
13 lut 18:04
Aagher: Okej teraz jestem, byłem przez chwile zajęty.
V(x)=(64−32x+4x2)x V(x)=4x3−32x2+64x
V1(x)= 12x2 −64x2 +64
Δ= 1024 √Δ=32 x=4 x2=1,3
13 lut 18:18
Aagher: x2 jest maksimum, więc objętość wynosi 37,9 litra.
Dziękuje bardzo pomoc.
13 lut 18:24
Mila:
13 lut 18:39

