TEST XIV
Blue: Bardzo prosiłabym, żeby ktoś sprawdził mi zad.11 i pomógł z tym drugim zadaniem dowodowym.
Zad.11 Dane są dwa okręgi o równaniach x
2+y
2=a−1 i x
2+y
2=5−a Wykaż, że iloczyn długości
promieni tych okręgów jest niewiększy od 2.
http://i57.tinypic.com/27wx5hi.jpg
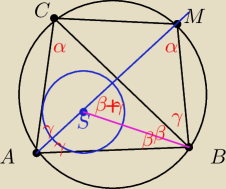
zad.13 W trójkącie ABC dwusieczna kąta A przecina okrąg opisany na tym trójkącie w punkcie M.
Punkt S jest środkiem okręgu wpisanego w trójkąt ABC. Udowodnij, że odcinki MS, MB i MC mają
tę samą długość.
http://i60.tinypic.com/2cctcnt.jpg
Z góry dziękuję z pomoc
PS tak w sumie to w tym pierwszym chyba dziedzina powinna być (1,5), no bo r musi być większy
od 0, ale nie wracajcie na to uwagi
13 lut 15:42
Blue:
13 lut 16:45
Qulka: 11 OK nad dwunastym dumam
13 lut 16:51
Qulka: MB i MC mają tę samą długość bo M leży na dwusiecznej a BiC na ramionach kąta
13 lut 16:54
Blue: Jak na coś wpadniesz, to daj znać
13 lut 16:54
Blue: ale pozostaje nam jeszcze MS
13 lut 16:56
Qulka: nad tym właśnie myślę
13 lut 16:58
wmboczek: poprowadź CS i z S prostopadłą do AC
Z rozpisania kąta półpełnego kąt CSM i można pokazać, ze jest taki sam jak CMS
13 lut 17:09
Tadeusz:
... kąty oparte na takiej samej cięciwie ... a skoro kąty są równe (dwusieczna) to i cięciwy
...
zatem MB=MC −
13 lut 17:09
Qulka: mam
13 lut 17:10
Qulka:
13 lut 17:13
Qulka: kąt CAM = kąt CBM bo wpisane na tej samej cięciwie
kąt ASB = 180−β−γ więc przyległy kąt BSM = β+γ
zatem trójkąt MBS równoramienny bo równe kąty przy podstawie
analogicznie do C
13 lut 17:15
Tadeusz:
skoro ∡MAC i ∡MAB są równe to |CM|=|BM|
13 lut 17:18
Qulka: a skąd wiesz że są równe
mi wychodzi że jeden to 2β a drugi to α
13 lut 17:32
Tadeusz:
... źle odczytujesz kąt ... skoro ∡MAC to jego wierzchołek to A
13 lut 18:16
Blue: Dziękuję Wam
A mam jeszcze takie pytanko zawsze prosta przechodząca przez wierzchołek i
środek okręgu wpisanego jest dwusieczną, tak?
13 lut 19:09
Mila:
Środek okręgu wpisanego w wielokąt leży na przecięciu dwusiecznych kątów wewnętrznych
wielokąta.
13 lut 19:26
Blue: Dzięki Milu
13 lut 20:05
Qulka:
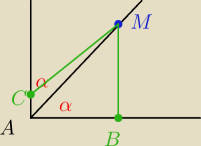
Tadeusz skoro z równości ∡MAC i ∡MAB wynika |CM|=|BM| to jak na tym rysunku to odczytać?
14 lut 00:04
Kacper:
Qulka to nie ta sama sytuacja
W zadaniu C oraz B położone są na okręgu
14 lut 12:01
Qulka: Na wszelki wypadek starałam sie tego nie zakładać chociaż wydawało mi się oczywiste
14 lut 12:08
15 lut 17:18
Mila:
Licz początkowe wyrazy ciągów wg podanych wzorów i będziesz wiedział.
15 lut 17:22
Eta:
A) → III
B)→ II
C)→ IV
D)→ I
15 lut 17:25
