stereometria kombinator: Bardzo proszę o pomoc jak zacząć. Dany jest ostrosłup prawidłowy czworokątny o wysokości 7 w którym kąt między ścianami bocznymi ma miarę 120 stopni. Jaka jest długość krawędzi podstawy ?

kombinator: .

yolex: Masz trójkąt o kącie 120stopni i bokach: przekątna podstawy i wysokości ścian bocznych (te od wierzchołka podstawy do krawędzi bocznej). Załóżmy, że podstawa ma długość 2a. Wtedy boki trójkąta a√2, 2a√6/√3 a jego wysokość a√6/√3( z własności trójkąta 30,60,90 albo trygonometria) Teraz inne trójkąty: wysokość bryły, przekatna podstawy (połowa) i krawędź boczna. W tym trójkącie masz trójkąt do niego podobny: wysokość bryły, wysokość tego trójkata o kącie 120 oraz kawałek krawędzi bocznej i drugi trójkąt, który zostaje z dużego przez wycięcie pierwszego. Boki tego górnego to 7, a√6/√3 i kawałek krawędzi bocznej − możesz policzyć z Pitagorasa. Boki małego, to a√2, a√6/√3 i kawałek krawędzi bocznej − ja policzyłam z Pitagorasa i wyszło mi 2a√3/3. Korzystając z podobieństwa piszesz proporcję − np. 7/{ 2a√6/√3}={a√2}/ {2a√3/3}. Stąd otrzymałam 2a=7 To tylko szkic rozwiązania i wymaga przeliczenia, ale może Ci pomoże. Rysunki w tym edytorze to koszmar i nie odważyłam się wstawiać.

yolex: Oczywiście się pomyliłam w pisaniu − na samym początku. Boki trójkąta to: 2a√2, 2a√6/3 a jego wysokość a√6/3 itd. I wszędzie, gdzie występuje w mianowniku pierwiastek z 3 powinna być sama trójka. To tylko błąd edycji − rachunki są dla dobrych wartości.

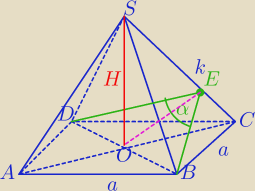
Mila: H=7 α=120 BE⊥SC i DE⊥SC Dobranoc, do jutra.