zadanie optymalizacyjne Archy: W kulę o promieniu długości R wpisano stożek o największej objętości. Jaka jest długość wysokości tego stożka?

Archy: ?

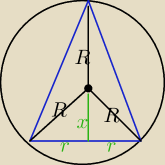
Qulka: x²+r²=R² więc r²=R²−x²

	π(R2−x2)•(x+R)
V=πr2•h/3 =		x∊(0;R)
	3

pochodna z V = 0 to ekstremum

Archy: ok dzięki mam jeszcze problem z tym zadaniem: w stożek, którego promień podstawy ma długość R, a wysokość H wpisano prostopadłościan o największej objętości. Stosunek długości krawędzi podstawy prostopadłościanu wynosi 2:1. Znajdź wymiary tego prostopadłościanu. wyliczyłem sobie długość podstawy a=²₃R, nie wiem tylko jak uzależnić od siebie wysokości

Qulka: z podobieństwa trójkątów H/R = h/pół przekątnej postawy

Archy: a w tym poprzednim zadaniu pochodna będzie f'(R) czy f'(x)?

Qulka: V'(x)