kąt ostry nelly: Wewnątrz kąta ostrego α znajduje się punkt odległy od jednego ramienia o a, od drugiego o b. Znaleźć odległość tego punktu od wierzchołka kąta.

nelly: up

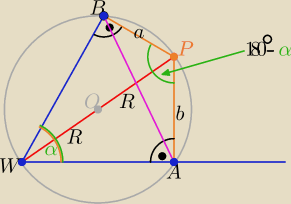
Eta: Z warunków zadania: na czworokącie APBW można opisać okrąg ( dlaczego? to |∡APB|=180^o−α to |WP|=2R

	|AB|
z tw.sinusów w trójkącie ABW :		=2R
	sinα

z tw. kosinusów w trójkącie APB : |AB|² = a²+b²−2ab*cos(180^o−α) ⇒ |AB|²=a²+b²+2ab*cosα |AB|=√a²+b²+2ab*cosα

	|AB|		√a2+b2+2ab*cosα
zatem |WP|= 2R=		=
	sinα		sinα

nelly: Można opisać okrąg, bo: 90 + 90 = 180 i α+180−α = 180

Eta: ok

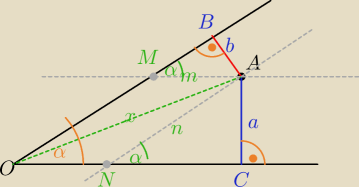
Mila: AM||OC⇒ W ΔABM:

	b		b
sinα=		⇔|AM|=m=
	AM		sinα

AN||OB

	a		a
sinα=		⇔|AN|=n=
	AN		sinα

Kąt α jest kątem ostrym w równoległoboku ONAM: Z tw. cosinusów: x²=m²+n²−2*m*n*cos(180−α)⇔

	b2		a2		a*b
x2=		+		+2*		*cosα⇔
	sin2α		sin2α		sin2α

	√a2+b2+2ab cosα
x=
	sinα

==========================

Eta:

pigor: ..., to może jeszcze kogoś zainteresuje np. tak : niech S wierzchołek danego kąta i P punkt wewnątrz niego taki, że |PA|=a, |PB|=b, |∡ASB|=α, |∡ASP|=β, to |∡ASB|=α−β,

	a		b
to (*) |PS| =		=		= ?⇔ a sin(α−β)=b sinβ ⇔
	sinβ		sin(α−β)

⇔ a sinαcosβ−a sinβcosα = b sinβ ⇔ a sinα√1−sin²β = (b+a cosα)sinβ /² ⇔ ⇔ a²sin²α(1−sin²β) = (b²+2abcosα+a²cos²α)sin²β ⇔ ⇔ (b²+2abcosα+a²cos²α)sin²β = a²sin²α − a²sin²αsin²β ⇔ ⇔ (b²+2abcosα+a²cos²α+a²sin²α) sin²β = a²sin²α ⇔ ⇔ (b²+2abcosα+a²(cos²α+sin²α)) sin²β = a²sin²α ⇔ ⇔ a²sin²α = sin²β (b²+2abcosα+a²) ⇒ a sinα = sinβ √b²+2abcosα+a²,

	a		√b2+2abcosα+a2
a stąd i(*)		=		=|PS|−szukana odległość.
	sinβ		sinα