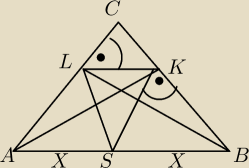
zdenerwowałem się! geometrykz: wykaż, że trójkąt... kurczę, 15 minut przepisywałem zadanie i znalazłem błąd na samym końcu, w trakcie przepisywania dlatego muszę już jakoś wykorzystać swoją obecność tutaj, podam co innego z czym też mam problem "odcinki ak i bl są wysokościami trójkąta ostrokątnego ΔABC, a punkt S jest środkiem boku AB. Uzasadnij, że trójkąt, którego wierzchołkami są punkty S, K, L jest rownoramienny". zauważyłem tyle: KS i LS to środkowe odpowiednio: ΔKAB oraz ΔABL, dodatkowo oba te trójkąty mają kąt prosty. to chyba za mało, żeby stwierdzić, że ΔKLS jest równoramienny. co dalej zrobić? jestem kiepski z planimetrii, nawet gorzej niż kiepski, proszę mi wybaczyć

Mila: Dobrze zacząłeś. KS− środkowa w prostokątnym ΔAKB poprowadzona z wierzchołka kąta prostego zatem jest równa

	1
promieniowi okręgu opisanego na tym Δ i jest równa		|AB| (AB− przeciwprostokątna).
	2

LS−środkowa w prostokątnym ΔALB poprowadzona z wierzchołka kąta prostego zatem jest równa

	1
promieniowi okręgu opisanego na tym Δ i jest równa		|AB|.⇔
	2

|KS|=|LS|⇔ ΔLKS jest trójkątem równoramiennym.

geometrykz: no tak! środkowa opuszczona na przeciwprostokątną z wierzchołka kąta prostego jest równa połowie tej przeciwprostokątnej, a przeciwprostokątna w okręgu opisanym na trójkącie tworzy średnicę − dobrze mówię? dzięki

Mila: