nierówności Pierdyk: Cześć mam pytanie ogólnie podnoszenia do potęgi przy nierównościach. np.: x−1<√7−x, czy w tym przypadku można podnieść do kwadratu obie strony?

piotrek: Nie można. wyznaczasz najpierw dziedzinę, czyli 7−x≥0 x≤7 Czyli dla x z tego przedziału lewa strona nierówności może być liczbą ujemną. Możesz podnieść gdy wiesz, że obie strony są dodatnie.

Pierdyk: to jak w takim razie można rozwiązać ów przykład.

Pierdyk: piotrek, pomozesz mi to rozwiązać, a może ty Mila ?

wmboczek: t=√7−x, t>0 lub do kwadratu pamiętając, że dla x<1 mamy prawdę

Pierdyk: czyli jednak nikt mi dalej nie pomoże ?

Mila: 1) x≤7 Sprawdzam lewą stroną. x−1≥0⇔x≥1 Dla x∊<1,7> obie strony nierówności są dodatnie, podnoszę obustronnie do kwadratu (x−1)²<7−x x²−2x+1−7+x<0 x²−x−6<0 Δ=25

	1−5		1+5
x=		lub x=
	2		2

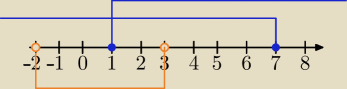
x=−2 lub x=3 ♦ x∊<1,3> Dla x<1 Prawa strona jest dodatnia ( z definicji pierwiastka kwadratowego) sprawdzamy co się dzieje z lewą stroną, gdy x<1, lewa strona nierówności jest ujemna, zatem mniejsza od wartości z prawej strony⇔ Rozwiązaniem nierówności jest każda liczba x∊(−∞,1)∪<1,3)⇔ x∊(−∞,3>

Mila: Co taki jesteś niecierpliwy. Pisanie zajmuje troche czasu.

Pierdyk: Dzięki wielkie i sorry za niecierpliwość. Trochę mi się spieszy, a chciałem to dobrze zrozumieć. A taki przykład jak rozwiązać? √x+3+√3x−2≤7

Mila: D

	2
x≥
	3

Masz obie strony dodatnie, możesz podnieść obustronnie do kwadratu, potem trzeba pomysleć.

Pierdyk: no właśnie. Z tym myśleniem dalej mi nie wychodzi, gdyż iż ciągle wychodzi pierwiastek. A podnoszenie dalej do potęgi to chyba bezsens. Chyba trzeba coś pod tym pierwiastkiem kombinować, czyż nie ?

Mila: Zostaw pierwiastek na jednej stronie, resztę na prawą strone, znowu założenie, że prawa≥0 i podnoś do kwadratu.

Mila: No i co?