Pochodne pomoc Szukający : Witam mam problem o to z takim zadankiem. Oblicz największą wartość funkcji f(x)=9x −x³ w przedziale <0,2> F(x)= −x³ +9x Liczę pochodną wychodzi mi jej wartość f1(x)= −3x² +9 xo= √3 xo2= −√3 F(0)=0 F(2)= 9*2 − 2³= 18−8=10 F(√ 3)= tu wychodzi mi błąd odpowiedz w książce wynosi 6√3 A ja to liczę 9√3 −9 Pomoże ktoś troszkę się pogubiłem i czy moja metoda jest dobra

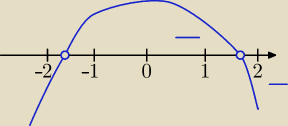
Mila: f'(x)=9−3x² f'(x)=0⇔ 9=3x² x²=3 x=√3 lub x=−√3 −√3∉<0,2> √3∊<0,2> Badamy czy f(x) ma maksimum lokalne w x=√3 9−3x²>0⇔3−x²>0 (√3−x)*(√3+x)>0 Przy przejściu przez x=√3 pochodna zmienia znak z dodatniego na ujemny⇔ Funkcja rośnie a potem maleje⇔w x=√3 f(x) ma maksimum lokalne f(√3)=9*√3−(√3)³=9√3−3√3=6√3

Szukający : Mam tylko pytanie co do obliczeń Dlaczego (√3)³= 3√3 ? Czy dobrze to rozumiem ? (3^/0,5)³= 3¹,5=3√3 Przepraszam troszkę za zapis, mało czytelny.

Mila: (√3)³=(√3)²*√3=3*√3 albo (√3)³=√27=√9*3=3√3

Szukający : Dzięki już wiem dlaczego tak jest.

Mila: