proszę o rozwiązanie Michał: udowodnij że dla każdego n ∊ N liczba 3⁴ⁿ⁺² = 1 jest podzielna przez 10 ja to zacząłem tak 3 ⁴ⁿ * 3² + 1 = (3²)ⁿ * 3² + 1 dalej nie wiem z czego jeszcze skorzystać

Mila: a=9*(3⁴)ⁿ+1=9*81ⁿ+1=10k, gdzie k∊N, ponieważ liczba 9*81ⁿ ma cyfrę jedności równą 9, zatem po dodaniu liczby 1 otrzymamy liczbę z cyfrą jedności 0⇔liczba a jest podzielna przez 10.

Saizou : albo tak 3⁴ⁿ⁺²=9²ⁿ⁺¹ 9≡−1 mod10 9²ⁿ⁺¹≡(−1)²ⁿ⁺¹≡−1 mod10 1≡1 mod10 =======+ 9²ⁿ⁺¹+1≡−1+1≡0 mod10 wiec 3⁴ⁿ⁺²+1 jest podzielne przez 10

Michał: dziękuję bardzo nie wiedziałem co zrobić z tą 1

Michał: Siatka ostrosłupa składa się z dwóch trójkątów równobocznych o boku długości 4 i z dwóch trójkątów prostokątnych Oblicz objętość tego ostrosłupa a otrzymany wynik przybliż z dokładnością 10⁻² i zakoduj go wynik to 754

Michał:

	1		1		a√3
V =		*		a*		* H a − krawędż podstawy ΔABC − jest trójkąt
	3		2		2

równoboczny dwie ściany są trójkątami prostokątnymi nie wiem jak obliczyć H

AS: W temacie zadania chyba jest błąd − powinno być 3^4*n+2 +1 3^4*n+2 +1 = (3⁴)ⁿ*3² + 1 = 81ⁿ*9 + 1 81ⁿ da zawsze na końcu cyfrę 1 a po pomnożeniu przez 9 cyfrę 9,Dodając do wyniku 1 końcówka będzie zerem, co świadczy już o podzielności przez 10.

Michał: to jest ten sam zapis 3^4*n+2

Michał: dziękuję bardzo

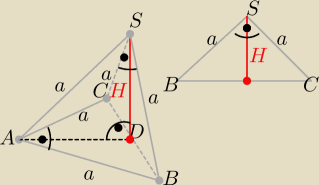
Eta: Podstawą trójkąt prostokątny równoramienny o ramieniu długości a=4 dwie ściany ABS i ACS −− trójkątami równobocznymi

	a√2
Ściana BCS trójkątem prostokątnym, w niej wysokość H =
	2

	a3√2
V=.....=		= ..........
	12

Michał: dziękuję bardzo

Eta: Na zdrowie ...