parametr m
Zdzisiu: Dla jakich wartości parametru m równanie:
mx2+(2m+1)x+m−1=0 ma dwa różne pierwiastki dodatnie?
Policzyłem praktycznie wszystko a wynik mi się nie zgadza z odp.
założenia:
delta>0
x1+x2>0
x1*x2>0
delta=8m+1
m>−1/8
teraz z wzorów viete'a
(−2m−1)/m>0
m(−2m−1)>0
m>0 lub −2m−1>0 −−−−−> −2m>1 −−−−−−> m<−1/2
(m−1)/m>0
m(m−1)>0
m>0 lub m−1>0 −−−−> m>1
co jest źle? końcowy przedział (odpowiedź) to m∊(−1/8;0)
12 lut 16:54
wmboczek: coś z tymi lubami nie tak
masz po prostu f kwadratową rozłożoną na czynniki, napisz poprawnie
12 lut 17:17
Mila:
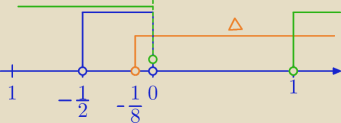
1)m≠0
(2m+1)*m<0 i
m*(m−1)>0
I teraz bawimy się w trzy kolory
12 lut 17:21
Zdzisiu: dzieki wielkie mila
12 lut 18:34
Zdzisiu: a tak mozna? ze przy niebiesksim mnoze razy −1 i sie zmienia znak?
12 lut 18:35
Mila:
−(2m+1) *m>0 to możesz zapisać:
(−1)*(2m+1)*m>0 /*(−1)⇔
(2m+1)*m<0
12 lut 18:39
Zdzisiu: a z zielonym ja rozisalem jako m>0 i m>1? dlaczego tam jest m <0?
12 lut 18:39
Mila:
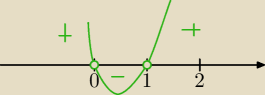
To jest nierówność kwadratowa.
m*(m−1)>0 parabola skierowana do góry
m<0 lub m>1
12 lut 18:50
Zdzisiu: więc z (2m+1)*m<0 jest:
m>0 lub m<−1/2 ?
12 lut 23:37
Mila:
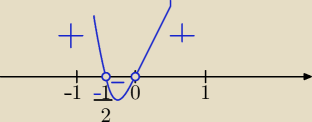
(2m+1)*m<0 ⇔
Powtórz nierówności kwadratowe.
12 lut 23:50
12 lut 23:51
Zdzisiu: przyda sie, dzieki
13 lut 12:01