podobieństwo
Karolina: Zadanie jest prawie rozwiązane, proszę tylko o wyjaśnienie pewnych rzeczy i dokończenie.
Zadanie:
Bok AB równoległoboku ABCD jest trzy razy dłuższy od boku BC. W jakim stosunku prosta
równoległa do boku BC podzieli bok AB, jeśli w wyniku podziału otrzymamy dwa równoległoboki, z
których jeden będzie podobny do równoległoboku ABCD?
LK− prosta równoległa do BC
AD/AB=AK/AD
k= AK/AD=1/3
AK/x=1/3
x=3 AK
AK=1/3x
1/3x / 3x = 1/3*1/3=1/9
1 pytanie − jak dokończyć ? 2 pytanie − jak myśleć, jakim tropem iść, żeby powstało te
podobieństwo AD/AB=AK/AD ? Bo jak robię bok krótszy' do krótszego, a dłuższy' do dłuższego (
zgodnie z teorią jaka się uczyłam ) to mi wychodzi AD/AB=AD/AK, co wiem, że jest źle, bo
wyszłoby że AB=AK , a nie jest równe. Proszę o wyjaśnienie , z góry dziękuję

12 lut 13:44
Qulka:
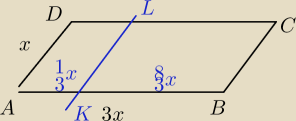
12 lut 13:55
Karolina: Czy mogłabyś wyjaśnić chociaż jakoś w skrócie jak obliczyłas 8/3 ?
12 lut 14:12
J:
| 1 | | 8 | | 9 | |
| x + |
| x = |
| x = 3x |
| 3 | | 3 | | 3 | |
12 lut 14:14
Karolina: Dobra, dziękuję bardzo

A na te drugie pytanie ktoś umiałby wyjaśnić?
12 lut 14:27
Qulka: jak widać na rysunku krótszy na górze do dłuższy na dole więc AD/AB = AK/AD
12 lut 14:29
J:
2) w AKLD bok krótszy AK musi być trzy razy mniejszy od dłuższego AD
12 lut 14:30
Karolina: Owszem z tego rysunku wszystko jasne. Ale gdybym odcinek KL zrobiła bliżej BC to ta zasada by
już nie obowiązywała. Wtedy wyszłoby AD/AB=AD/AK . W czym źle to rozumuje, jakbyś mogła coś
podpowiedzieć ?
12 lut 14:34
Qulka: wtedy nie wyszłyby podobne

a taki masz warunek w zadaniu

jak sama mówisz albo jest to
AB=AK więc ten sam albo musisz przysunąć tak blisko, żeby ten był krótszy innej możliwości nie
ma
12 lut 14:36
Karolina: Rety, naprawdę, dziękuję Ci bardzo. Głowilam się nad tym wczoraj prawie cały dzień. To jeszcze
się dopytam, czy to oznacza, że przy tego typu zadaniach powinnam uwzględnić też opcje że AK
jest dłuższy niż połowa AB i ja odrzucić właśnie poprzez napisanie ze AB nie może być równe
AK? Czy nie muszę tego pisać ? I czy jest taka opcja że będą izometrią, czyli podobieństwem w
skali 1 ?
12 lut 14:45
Qulka: skoro masz otrzymać DWA równoległoboki to tę opcję musisz odrzucić na wstępie podczas analizy
zadania

12 lut 14:57
Karolina: Racja, to że jest izometrią to odrzucam jeśli chodzi o to zadanie. A to, że AK nie może być
dłuższy niż połowa AB muszę pisać? Np. poprzez taki rysunek + proporcje AD/AB=AD/AK i
napisanie że AB nie może być równe AK . Czy tego się nie pisze ?
12 lut 15:15
Qulka: nie musisz

to oczywiste

12 lut 15:33
Karolina: Ok. A np. jak mam takie zadanie : W równoległoboku ABCD bok AB jest 2 razy dłuższy od boku AD.
Na boku AB zaznaczono punkt K, na boku DC punkt L w taki sposób że czworokąt AKLD jest podobny
do równoległoboku ABCD. Wyznacz skalę podobieństwa. Jak mam takie zadanie, to powinnam
przyjąć opcje, że będą izometrią? ( umiem całe to zadanie dzięki Tobie , jedynie nad tym
pytaniem się zastanawiam z izometrią i tylko o nie pytam

)
12 lut 15:45
Qulka: izometria to przystawanie, a one są tylko podobne
12 lut 15:52
Karolina: Izometria jest też podobieństwem o skali 1
12 lut 15:59
Karolina: Wtedy narysowałabym KL na boku BC.
12 lut 16:01
Qulka: to w takich zadaniach pomijasz
12 lut 16:02
Karolina: Szkoda że nie piszą takich szczegółów w podręcznikach . Jakbym Cię znała to dużą czekoladę już
ode mnie byś miała. Dziena

12 lut 16:10
Qulka: to zależy czy chcesz umieć rozwiązywać typowe zadania czy wgłębiać się w teorie.
ja matematykę traktuję strasznie po macoszemu i w normalnym życiu nie jest mi potrzebne
wgłębianie się w niuanse, ale puryści matematyczni uwielbiają właśnie zagadki a co by było
gdyby potraktować to bardziej lub mniej dosłownie i rozpatrują wszystkie skrajne przypadki.
Więc te szczegóły ściśle zależą od kierunku w jakim będziesz podążać i dlatego nie piszą ich w
podręcznikach.

12 lut 16:19
Karolina: Jak ja troche "wyluzuje" to potem sie okazuje ze nie umiem. Wiec wole juz zrozumiec doglebniej.
Ty za to masz dar do tłumaczenia. Studiujesz pewnie matematykę?
12 lut 16:58
Qulka: nie

tylko uwielbiam sobie upraszczać złożone rzeczy

12 lut 21:32
Karolina: O tak muszę potrenować tę umiejętność, bez niej ciężko w życiu. Pozdrawiam

13 lut 00:16


 A na te drugie pytanie ktoś umiałby wyjaśnić?
A na te drugie pytanie ktoś umiałby wyjaśnić?
 a taki masz warunek w zadaniu
a taki masz warunek w zadaniu  jak sama mówisz albo jest to
AB=AK więc ten sam albo musisz przysunąć tak blisko, żeby ten był krótszy innej możliwości nie
ma
jak sama mówisz albo jest to
AB=AK więc ten sam albo musisz przysunąć tak blisko, żeby ten był krótszy innej możliwości nie
ma

 to oczywiste
to oczywiste 
 )
)


 tylko uwielbiam sobie upraszczać złożone rzeczy
tylko uwielbiam sobie upraszczać złożone rzeczy 
