 POCHODNA
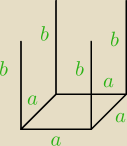
Wyznacz wymiary zbiornika w kształcie prostopadłościanu o podstawie kwadratowej i objętości
32m3
tak,aby suma pól ścian bocznych i podstawy była jak najmniejsza.
więc
V= 32m3
V= a*a*b = a2b
a2b= 32
POCHODNA
Wyznacz wymiary zbiornika w kształcie prostopadłościanu o podstawie kwadratowej i objętości
32m3
tak,aby suma pól ścian bocznych i podstawy była jak najmniejsza.
więc
V= 32m3
V= a*a*b = a2b
a2b= 32
| 32 | ||
b= | ||
| a2 |
| 32 | ||
P = a2 + 4a* | ||
| a2 |
| 128 | ||
P = a2 + | ||
| a |
| a3 + 128 | ||
P = | ||
| a |
| a3 + 128 | ||
P(a) = | ||
| a |
| 2a3 − 128 | ||
P'(a) = | ||
| a2 |
| 2a3 − 128 | |
> 0 | |
| a2 |
