podobieństwo Karolina: Zadanie jest rozwiązane, ale nie rozumiem dlaczego pewne rzeczy są tak a nie inaczej. W równoległoboku ABCD bok AB jest 2 razy dłuższy od boku AD. Na boku AB zaznaczono punkt K, na boku DC punkt L w taki sposób że czworokąt AKLD jest podobny do równoległoboku ABCD. a) Wyznacz skalę tego podobieństwa b) Oblicz AK:KB AB/AD =AD/AK, ( moje pytanie czemu AD do AK ? W ogóle skąd ta proporcja, na jakiej podstawie powstała?)czyli 2x/x =x/AK 2x *AK =x2, (x kwadrat) AK =x2/(2x) AK =x/2 Skala podobieństwa "k': k =AK/AD k =x/2 :x =1/2 Odp.Skala podobieństwa 1/2

MateMax: Odcinek LK jest równoległy do AD

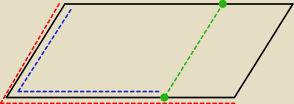
Eve: ABCD∼AKLD⇒ta proporcja ( zgodnie z kolorami)

Karolina: Dziękuję bardzo A jeszcze zastanawia mnie czy proporcje można ułożyć jakoś inaczej jeszcze. Bo w szkole uczyliśmy się ze bok podobny do boku oryginalnego , a tu inaczej i to mnie dziwi .

Karolina: Już rozkminilam wszystko dokładnie. Jeszcze raz dziękuję bardzo

Eve: w proporcji można zmieniać wyrazy

Karolina: Ja ogólnie to zrobiłam tą prostą LK równoległa do AD bliżej BC. Czy wtedy jest zle czy to bez różnicy?

Karolina: Tzn. tak jak na twoim rysunku zrobiłam. A jak zrobiłam bliżej AD to wtedy mi wyszły proporcje. Bo krótszy' do krótszego i dłuższy' do dłuższego. Ta zasadą się kieruję przy podobieństwach

Karolina: A jak zrobiłam bliżej BC to już tego nie ogarniam czemu te proporcje są dobre.

Karolina: A może jest taka zasada, że jak jest czworokat, który ma wszystkie boki równoległe, to czworokat podobny do niego, jest tylko wtedy, gdy ten podobny czworokat jest mniejszy niż połowa oryginalnego? Wtedy by było wszystko jasne, a jeśli nie to tego drugiego sposobu co narysowała Eta nie rozumiem.

Karolina: Eve*

Karolina: Wychodzi mi zgodnie z tą zasadą krótszy' do krotszego i dłuższy' do dłuższego AB/AK = AD/AD. W czym moje rozumowanie jest złe ?

Eve:

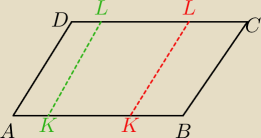
	AD		AK		AB		AD
z zielonym:		=		⇒		=
	AB		AD		AD		AK

	AD		AD
z czerwonym:		=		⇒AB=AK, więc mój błąd
	AB		AK

	AD		AK
ma być		=
	AB		AD

Karolina: A no właśnie i zielonym jest : ( dłuższy do krótszego = dłuższy do krótszego) a czerwonym jest: ( krótszy do dłuższego = dłuższy do krotszego ). Jaka jest zasada na proporcje ? Bo ta moja jest zła.

Karolina: Jedyne co wykombinowalam to z twierdzenia o stycznej i o siecznej mi wychodzą te proporcje : |AD|² = |AK| * |AB| −−−> |AD|=(|AK|*|AB| ) / |AD| = |AD|/|AK|=|AB|/|AD| . Ale czy nie przekombinowalam, czy to jest poprawne? A może jest na to lepszy sposób ?

Karolina: A może chodzi o to, że : jedna podstawa razy druga podstawa = jedno ramię razy drugie ramię . I z tego się układa proporcje

Karolina: I jeszcze jedno pytanie czy to ma jakieś znaczenie czy napiszę |KA| czy |AK| albo |AD| czy |DA| itp. ?

Karolina: jak te proporcje tworzyć żeby się nie pomylić i nie zrobić np. AD/AB=AD/AK? Wiem, że to źle, bo wtedy wyszłoby, że AK i AB są takie same a to nieprawda. Wymyśliłam że może robic zawsze ramię jednego razy ramię drugiego podobnego boku = podstawa jednego razy podstawa drugiego podobnego boku . ?