 ΔABC jest podobny do ΔBEF z cechy BKB, zatem ΔBEF jest równoboczny. Ponieważ kąt płaski, to kąt
zawarty między ramionami Δ równoramiennego, zatem BE=BF=EF=a2.
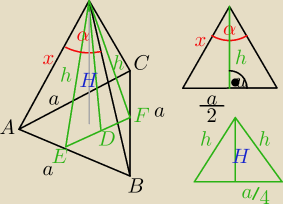
Teraz spójrz na rysunek w prawym górnym rogu:
ΔABC jest podobny do ΔBEF z cechy BKB, zatem ΔBEF jest równoboczny. Ponieważ kąt płaski, to kąt
zawarty między ramionami Δ równoramiennego, zatem BE=BF=EF=a2.
Teraz spójrz na rysunek w prawym górnym rogu:
| h | ||
ctgα2 = | ||
| a2 |
| a * ctgα2 | ||
h= | ||
| 2 |
| EF | ||
DF= | ||
| 2 |
| a | ||
DF= | ||
| 4 |
| a | ||
H2 + ( | )2 = h2 | |
| 4 |
| a2 | ctg2α2 * a2 | |||
H2+ | = | |||
| 16 | 4 |
| ctg2α2 * a2 | a2 | |||
H2 = | − | |||
| 4 | 16 |
| 4ctg2α2 * a2 − a2 | ||
H2 = | ||
| 16 |
| a2 * (4ctg2α2 − 1) | ||
H2 = | ||
| 16 |
| a * √4ctg2 α2 − 1 | ||
H2 = | ||
| 4 |
| 1 | a | a * √4ctg2 α2 − 1 | ||||
P = | * | * | ||||
| 2 | 2 | 4 |
| a2 * √4ctg2 α2 − 1 | ||
P = | ||
| 16 |
| a2 * √4(ctg2 α2 − 14) | ||
P = | ||
| 16 |
| 2a2 | ||
P = | √ctg2α2 − 14 | |
| 16 |
| a2 | ||
P = | √ctg2α2 − 14 | |
| 8 |
 .
.