trójkąt sillyboy: Dla jakich x istnieje trójkąt o bokach a=log2, b=log(2^x +1) , c=log (2^x + 2) ?

Dziadek Mróz: a + b > c a + c > b b + c > a a = log(2) b = log(2^x + 1) c = log(2^x + 2) a + b > c log(2) + log(2^x + 1) > log(2^x + 2) log(2(2^x + 1)) > log(2^x + 2) 2^{x + 1} + 2 > 2^x + 2 2^{x + 1} > 2^x x + 1 > x 1 > 0 x ∊ ℛ a + c > b log(2) + log(2^x + 2) > log(2^x + 1) log(2(2^x + 2)) > log(2^x + 1) 2^{x + 1} + 4 > 2^x + 1 2^{x + 1} − 2^x > −3 2^x(2 − 1) > −3 2^x > −3 x ∊ ℛ b + c > a log(2^x + 1) + log(2^x + 2) > log(2) log((2^x + 1)(2^x + 2)) > log(2) 2^2x + 2^{x + 1} + 2^x + 2 > 2 2^2x + 2^{x + 1} + 2^x > 0 2^x(2^x + 2 + 1) > 0 2^x > 0 x ∊ ℛ Sprawdzenie dla x = 1: a = log(2) b = log(2^x + 1) = log(2 + 1) = log(3) c = log(2^x + 2) = log(2 + 2) = log(4) a + b > c log(2) + log(3) > log(4) 6 > 6 a + c > b log(2) + log(4) > log(3) 8 > 3 b + c > a log(3) + log(4) > log(2) 12 > 2

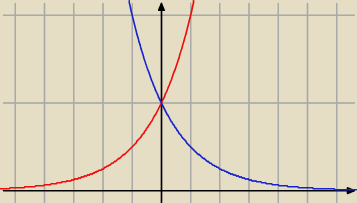
Dziadek Mróz: a^b > 0 zawsze f(x) = 2^x g(x) = 2^−x

sillyboy: Dzięki wielkie