Jak naszkicować w układzie OXY bryłę
Kin: Hej
Jak naszkicować w układzie OXY bryłę, powstałą z obrotu linii będącej wykresem funkcji
Proszę o podpowiedź
11 lut 11:37
Eve:
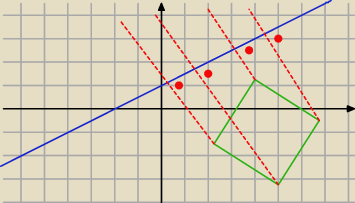
przekształć symetrycznie
11 lut 11:41
J:
tu chyba ma się obracać ta prosta
11 lut 11:45
Eve: własnie nie bardzo zrozumiałam zadanie, a ta prosta to wokół osi? jednej, dwóch, co to zgaduj
zgadula?
11 lut 11:47
Eve:
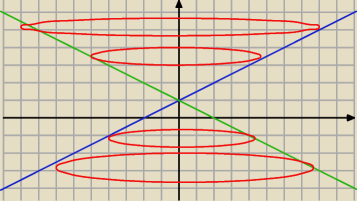
11 lut 11:51
Godzio:
I nie jest powiedziane nawet wokół której osi ...
11 lut 11:53
Kin: Polecenie dokładnie:
Obliczyć objętość bryły powstałej z obrotu linii będącej wykresem funkcji:
| | 1 | |
y = |
| x+1, dla x∊ <0,1> |
| | 2 | |
Naszkicować w układzie OXY wskazaną bryłę.
11 lut 11:55
J:
naucz się pisać całą treść zadania , nikt tu nie jest jasnowidzem !
11 lut 11:56
Kin: Teraz jest cała treść zadania. Nie sądzicie że facet nie sprecyzował czego od nas oczekuje ?
11 lut 11:58
Eve: wokół czego?
11 lut 11:58
J:
| | 1 | |
V = π∫( |
| x+1)2dx w granicach: <0,1> |
| | 2 | |
11 lut 11:59
J:
po zkresie widać,że wokół osi OX
11 lut 11:59
J:
postała bryła , to stożek ściety o osi OX
11 lut 12:00
Eve:
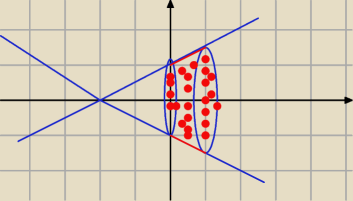
coś takiego
11 lut 12:04
Dziadek Mróz:
| | 1 | | 1 | | x3 | | x2 | |
V = π0∫1( |
| x + 1)2dx = π0∫1( |
| x2 + x + 1)dx =π[ |
| + |
| + x]0|1 |
| | 2 | | 4 | | 12 | | 2 | |
=
| | 1 | | 1 | | 1 | | 6 | | 12 | | 19 | |
= π( |
| + |
| + 1) = π( |
| + |
| + |
| ) = π |
| |
| | 12 | | 2 | | 12 | | 12 | | 12 | | 12 | |
11 lut 12:20