geometria analityczna, jednokładność Arko: Proszę o pomoc, wyjaśnienie w jaki sposób, jaką metodą rozwiązuje się tego typu zadania Okrąg O1 o środku w punkcie (4,−2) jest styczny do osi OX. Okrąg ten przekształcono przez jednokładność o skali k=−3/2 i środku w punkcie P, należącym do prostej y=−1/2x. W ten sposób otrzymano okrąg O2, podaj równanie tego okręgu gdy: a) jest on styczny do osi OX b )jest on styczny do osi OY W przykładzie a) obliczyłem, że r1=2, r2=3 p(x,−1/2x)

5-latek: Najlepiej zrobic rysunki . naprawde

Arko: nie rozumiem w jaki sposób to zrobić, pomoże ktoś

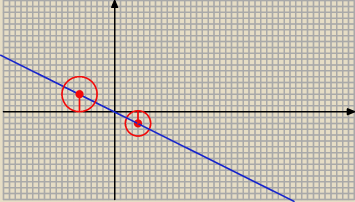
Janek191: a) O₁ = ( 4; − 2) − środek danego okręgu Okrąg jest styczny do osi OX, więc r₁ = 2

	3
k = −		= − 1,5
	2

więc r₂ = I k I*r₁ = 1,5*2 = 3 Mamy

x1		− x2
	=
r1		r2

4		−x2
	=		⇒ x2 =− 6
2		3

y₂ = k*y₁ = −1,5*(−2) = 3 więc O₂ = ( −6 ; 3) Równanie okręgu jednokładnego do danego: ( x + 6)² + ( y − 3)² = 3² =====================

wmboczek: S'=P+k(SP→) a) druga wsp będzie +/− r2 a) pierwsza wsp będzie +/− r2

Janek191: a) O₁ = ( 4; − 2) − środek danego okręgu Okrąg jest styczny do osi OX, więc r₁ = 2

	3
k = −		= − 1,5
	2

więc r₂ = I k I*r₁ = 1,5*2 = 3 Mamy

x1		− x2
	=
r1		r2

4		−x2
	=		⇒ x2 =− 6
2		3

y₂ = k*y₁ = −1,5*(−2) = 3 więc O₂ = ( −6 ; 3) Równanie okręgu jednokładnego do danego: ( x + 6)² + ( y − 3)² = 3² =====================

Arko: dziękuję bardzo

Janek191: Uwaga: Ta proporcja jest prawdziwa, bo prosta o równaniu y = − 0,5 x przechodzi przez punkt O = (0; 0), czyli O jest środkiem jednokładności