Rozwiąż algebraicznie i graficznie układ równań Patryk: Rozwiąż algebraicznie i graficznie układ równań:

⎧	|x|+|y|=5
⎩	xy=6

Nakierujcie mnie jak to robić Dobrze rozumuje, że należy to rozpatrzyć dla 4 przypadków? Czy jest jakaś inna metoda? 1. x≥0 i y≥0 2. x≥0 i y<0 3. x<0 i y≥0 4. x<0 i y<0 1.

⎧	x+y=5
⎩	xy=6

⎧	x=5−y
⎩	(5−y)y=6

−y²+5y−6=0 Δ=25−24=1 ⇒√Δ=1

	−6		−4
y=		=3 ⋁ y=		=2
	−2		−2

⎧	y=3
⎩	x=2

lub

⎧	y=2
⎩	x=3

No i następnie dla przypadków 2−4, po czym umieścić te punkty na układzie współrzędnych?

Eve: nie ma innej, dobrze robisz, ale jeśli xy=6, to dla x, y przeciwnych znaków przypadki odpadają

Patryk: Okej, rozumiem, dzięki Taki myk, że źle z książki przepisałem i jest xy=−6, czyli odpadają przypadki, że jak są jednakowe znaki, to odpadają, ta?

Patryk: Jak ja pisze...

Eve: tak odpada x,y tych samych znaków

Patryk: Dzięki (2−gi dzień z rzędu) i pozdrawiam

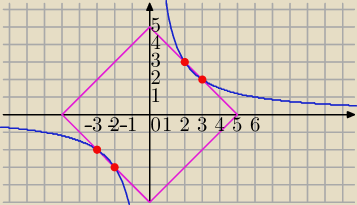
Mila: 1) Metoda graficzna : |x|+|y|=5

	6
y=
	x

(−3,−2),(−2,−3),(2,3),(3,2) 2) Metoda algebraiczna |x|+|y|=5 x*y=6 /:x x≠0 bo x*y≠0

	6
y=		,
	x

	6
|x|+|		|=5 /*|x|
	x

x²−5|x|+6=0 Wyznaczam |x| z równania, |x|≥0 Δ=1

	5−1		5+1
|x|=		lub |x|=
	2		2

|x|=2 lub |x|=3⇔ x₁=2 lub x₂=−2 lub x₃=3 lub x₄=−3 y₁=3 lub y₂=−3 lub y₃=2 lub y₄=−2 ===============================

Patryk: A więc to o to chodziło w metodzie graficznej... No i algebraiczną idzie uprościć. Nie wiem Mila, czy to przeczytasz, ale dziękuję bardzo

Mila: Ważne, abyś z tego skorzystał.

Patryk: Jasne, przed chwilą (po godzinie pauzy) zrobiłem to Twoim sposobem − i się udało. Mam kolejne: Zaznacz w układzie współrzędnych zbiór wszystkich punktów (x,y), których współrzędne spełniają nierówność: y²+x²≤2|x|y y²−2|x|y+x²≤0 ♦ dla x≥0 x²−2xy+y²≤0 (x−y)²≤0 Aby równanie było mniejsze lub równe 0, to: y=x ♦ dla x<0 x²−2(−x)y+y²≤0 x²+2xy+y²≤0 (x+y)²≤0 A tutaj co? y= Następnie narysować w przedziale x≥ prostą o równaniu y=x i w przedziale x<0 to czego nie wiem?

Mila: x+y=0⇔ y=−x

Patryk: Ehh... za dużo matmy na dziś. Dziękuję