nierówność
john2: Jak pokazać, że prawdą jest taka nierówność: x2 − ln(x2) ≥ 0 ?
10 lut 18:34
wmboczek: np wyznaczyć minima lokalne i granice
10 lut 18:47
john2:
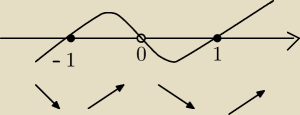
Tak?
f(x) = x
2 − ln(x
2)
| | 2 | | 2x2 | | 2 | | 2x2 − 2 | | x2 − 1 | |
f'(x) = 2x − |
| = |
| − |
| = |
| = 2 * |
| = |
| | x | | x | | x | | x | | x | |
Wartości funkcji w minimach:
f(−1) = 1 − 0 = 0
f(1) = 1 − 0 = 0
a po co te granice?
10 lut 18:58
john2: Granice by były konieczne, gdyby funkcja malała "w kierunku" krańców dziedziny?
10 lut 19:05
Gray: Albo tak: dla funkcja f(x)=lnx oraz dla x>0 mamy ze wzoru Taylora:
| | f''(c) | | 1 | |
lnx= f(x) = f(1) + f'(1)(x−1) + |
| (x−1)2 = x−1 − |
| (x−1)2≤ x−1≤x. |
| | 2 | | 2c2 | |
Podstawiając za x → x
2 mamy tezę: lnx
2≤x
2
10 lut 22:22
john2: Dzięki.
10 lut 22:26