mleko
Mieszko I: Moi poddani!
supcio zadanko o pochodnej zapraszam
Wyznacz przedziały monotoniczności i ekstrema funkcji f(x)= x
5 − 15x
3.
Zbadaj liczbę rozwiązań równania f(x)=m w zależności od parametru m.
ready steady go
f'(x)= 5x
4 − 45
2
5x
4 − 45
2 = 0
5x
2(x
2 − 9) = 0
5x
2(x−3)(x+3) = 0
f'(x) > 0
x∊ (−
∞,−3)∪(3,+
∞)
f'(x) < 0
x∊ (−3,3)
pytanko: w odpowiedzi mam przedziały zamknięte...why?
f(−3) = 162 MAX
f(3) = −162 MIN
ok i co dalej z tym parametrem? sugestie?

10 lut 16:15
Bolesław Chrobry: Ojcze!
pomóc Ci nie zdołam,ale pomoc jest już w drodze!
o ludzie! pomóżcie!
chwała po wszystkie czasy za rozwiązanie tego piekielnego zadania!
10 lut 16:40
Abey: Poproś Dobrawe

10 lut 16:45
Mieszko I: Ludu,mój ludu!
10 lut 18:52
Frost: Musisz narysować przybliżony wykres tej funkcji a potem ciąć ją prostą równoległą do osi OX i
zapisywać liczbę rozwiązań
10 lut 18:54
Mieszko I: a mój przyjacielu,co z tymi przedziałami? otwarte czy zamknięte?
10 lut 18:57
Janek191:
f '(x) = 5 x4 − 45 x2 = 5 x2*( x2 − 9) = 5 x2*( x − 3)*( x + 3)
10 lut 18:59
Mieszko I: bracia,moglibyście to narysować?

11 lut 16:08
john2:
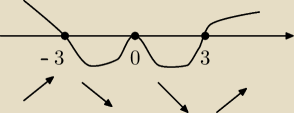
11 lut 16:34
john2: Jeśli nie pytają o maksymalne przedziały mono, to otwarte.
11 lut 16:34
john2: Aha. Nie doczytałem. Moment.
11 lut 16:38
john2:
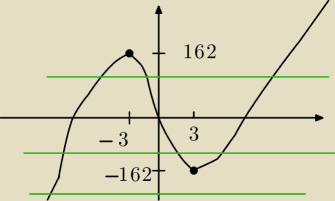
no i np. dla m ∊ (162,+
∞) mamy jedno rozwiązanie.
dla m = 162 dwa
itd.
11 lut 16:46




 no i np. dla m ∊ (162,+∞) mamy jedno rozwiązanie.
dla m = 162 dwa
itd.
no i np. dla m ∊ (162,+∞) mamy jedno rozwiązanie.
dla m = 162 dwa
itd.