wyznacz przedzialy monotonicznosci mezzo : wyznacz przedzialy monotonicznosci y= ³√(x²−2x)²= (x²−2x)^2/3 a wiec wyznaczam dziedzine funkcji Df=R czy dobrze? nastepnie licze pochodna

	2		1
y'=)		*		*(2x−2) Df'= (−∞;0)u(0;2)u(2;+∞)
	3		3√x2−2x

2		1
	*		*(2x−2)=0
3		3√x2−2x

2*(2x−2)=0 x=1 nie wiem teraz jak namalowac wykres aby dobrze wyznaczyc przedzialy ? prosze o pomoc !

J: nie musisz nic malować, sprawdź , czy pochodna zmienia znak w punkcie: x = 1

mezzo : ale jak to sprawdzic ?

J:

	1		3
policz np. f'(		) oraz f'(		)
	2		2

mezzo : a co z punktami krancow przedzialu dziedziny pochodnej ?

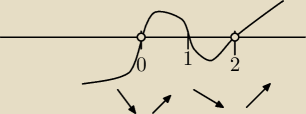
john2: Jeśli chcesz przybliżony wykres pochodnej, narysuj go na podstawie rozwiązań tych nierówności:

x − 1
	> 0
3√x2 − 2x

x − 1
	< 0
3√x2 − 2x

mezzo : juz nie wiem jak wyznaczyc te przedziały czy moglby mi ktos to rowziazac

john2:

x − 1
	> 0 / * (3√x2 − 2x)2
3√x2 − 2x

(x − 1) * ³√x² − 2x > 0 (x − 1) * ³√x(x − 2) > 0

john2: Jeśli ekstrema też masz wyznaczyć, zauważ również, że punkty x = 0 i x =2 należą do dziedziny naszej funkcji (choć nie należą do dziedziny pochodnej).