:)
kakak: Obliczyć pole obszaru ograniczonego krzywymi y= x + 2, y= x2 − 4. Proszę bardzo o całe
rozwiązanie. Z góry wielkie dzięki !
10 lut 13:32
Dziadek Mróz:
Jaki jest wzór na to pole?
10 lut 13:34
Krystek:
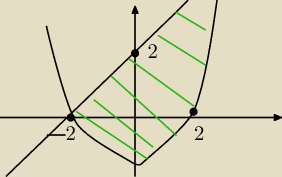
10 lut 13:35
10 lut 13:36
10 lut 13:36
Dziadek Mróz:
WBIĆ DO GŁOWY WZÓR:
Dla dwóch funkcji f(x) i g(x), gdzie a i b to wynik działania f(x) = g(x) pole między tymi
funkcjami:
P = a∫b[f(x) − g(x)]dx
10 lut 13:38
kakak: dzięki, ale samym rysunkiem nie zaliczę przedmiotu... rozwiązanie pliss !
10 lut 13:41
Krystek: ale my nie zaliczamy tylko Ty!
10 lut 13:43
Basia: a masz odpowiedzi ? wyszło mi 125/6 tylko nie wiem czy dobrze a jesli tak to napisze Ci rozw

10 lut 13:43
J:
masz podana całkę w linku powyżej ... potrafisz ją obliczyć ?
10 lut 13:43
kakak: nie mam rozwiązania niestety... ale jakbyś mogła wstawić, przynajmniej będę wiedzieć w jakimś
iść kierunku i dojdę do wszystkiego po kolei

Fajnie,że ktoś rozumie.

Jakbym umiała rozwiązać to zadanie, to chyba bym nie prosiła o pomoc? Bo fajnie jest sobie zrob
to i to dla kogos kto jest zielony w tym temacie...
10 lut 13:50
Basia: −2∫3 (x+2−(x2−4)dx=[−1/3x3+1/2x2+6x]3−2=125/6+C
10 lut 13:54
Basia: najpierw podstawiasz 3 pod x pożniej −2 i odejmujesz

Powodzenia !
10 lut 13:58
Dziadek Mróz:
PODSTAWY CAŁEK:
∫F(x)dx = f(x)
∫(F(x) ± G(x))dx = ∫F(x)dx ± ∫G(x)dx = f(x) + g(x)
a∫bF(x)dx = f(b) − f(a)
10 lut 14:14
kakak: y=x+2, y=x2 − 4
x+2 = x2 − 4
x2 − x − 6 = 0
Δ = 25 √Δ = 5
x1 = 3 ∨ x2 = −2
" −2∫3 (x+2−(x2−4)dx=[−1/3x3+1/2x2+6x]3−2=125/6+C "
a teraz jak liczę te całkę to ma znaczenie którą od której odejmę? I to drugie rownanie skad
sie wzielo?
10 lut 15:17
Basia: tak odejmujesz górną funkcje od dolnej czyli patrząc na wykres x+2−(x*2−4)
tak jak podał Dziadek Mróz
∫(F(x) ± G(x))dx = ∫F(x)dx ± ∫G(x)dx = f(x) + g(x)
Twoją fukcją F(x) jest x+2
G(x) = x
2−4
mam nadzieje że pomogłam

10 lut 15:44


 Fajnie,że ktoś rozumie.
Fajnie,że ktoś rozumie.  Jakbym umiała rozwiązać to zadanie, to chyba bym nie prosiła o pomoc? Bo fajnie jest sobie zrob
to i to dla kogos kto jest zielony w tym temacie...
Jakbym umiała rozwiązać to zadanie, to chyba bym nie prosiła o pomoc? Bo fajnie jest sobie zrob
to i to dla kogos kto jest zielony w tym temacie...
 Powodzenia !
Powodzenia !
