s
ger: Oblicz pole obszaru ograniczonego wykresem funkcji y = −x2 − x + 2 z osią OX.
Jak to zrobić ? Bo żeby było normalnie pole obliczyć to wiem. z całki nieoznaczonej, a co z tą
osią OX zrobić ?
10 lut 11:14
J:
nic , pozwoli Ci na wyznaczenie granic całkowania
10 lut 11:16
ger: czyli tak jak mówię liczyć ?
10 lut 11:18
ger: ale jak to narysować ? bo zawsze miałem dwie krzywe i miałem pole obszaru ,a tutaj jak jedna
krzwa to gdzie reszta pola ?
10 lut 11:22
Janek191:
y = − x
2 − x + 2 = 0
Oblicz: x
1 i x
2
10 lut 11:22
Dziadek Mróz:
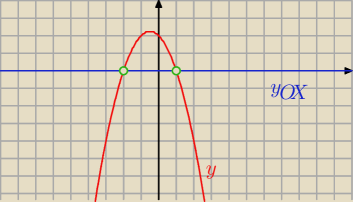
Wzór osi OX: y
OX = 0
y = −x
2 − x + 2
y = y
OX
−x
2 − x + 2 = 0
Δ = b
2 − 4ac = 1 + 8 = 9
| | −b ± √Δ | | 1 ± 3 | |
x1/2 = |
| = |
| |
| | 2a | | −2 | |
−2∫
1[−x
2 − x + 2]dx = ...
10 lut 11:23
J:
to pole między krzywą i osią OX
10 lut 11:23
Janek191:
x1 < x2
x2
P = ∫ f(x) dx
x1
10 lut 11:23
ger: mi wychodzi x1 = −1 i x2 = 1
bo podstawiałem bo tą funkcję y
10 lut 11:25
J:
to jest problem, bo chcesz całkować, a nie potrafisz obliczyc miejsc zerowych trójmianu
kwadratowego
10 lut 11:29
ger: dobra ok już ogarniam całka wynosi:
| | x3 | | x2 | |
− |
| − |
| + 2x dobrze ?> |
| | 3 | | 2 | |
10 lut 11:30
J:
tak
10 lut 11:32
Janek191:
Dobrze, ale pisz porządnie
10 lut 11:32