problem z lim mateusz: Witam. Mam pewien problem z granicami. Wowczas kiedy mamy sytuacje ze dana jest funkcja jakims wzorkiem przy x−−> 2 ( zalozmy). I chce sie dowiedziec w jakim przypadku bedziemy zwyczajnie podstawiac 2 do wzoru za ''x'' i liczyc kolejno granice za pomoca de' lhospitala lub innymi sposobami a kiedy bedziemy brac granica prawo i lewostronna i liczyc gdy x−−> 2+ i gdy x−−> 2− ? Prosze o odp. Prosze mi rowniez powiedziec co w przypadku gdy raz granica wychodzi +nieskonczonosc zalozmy przy jakims x−−> 1+ a raz wynosi −nieskonczonosc przy x−−> 1− bede wdzieczny za odp , pozdrawiam

Ada: 1. wstawiasz x, kiedy nie wychodzi ci osobliwość (nieskończoność, albo zero)

	∞		0
2. de l'Hospital kiedy masz symbol nieoznaczony typu:		,		(inne symbole
	∞		0

nieoznaczone można przekształcić do tej postaci) hmm... w zasadzie tej reguły nie odkrył raczej de l'Hospital

	jakaś liczba
3. kiedy masz coś takiego		, bo wtedy wiesz, że to dąży do nieskończoności,
	0

określasz tylko jej znak.

mateusz: noo i wtedy biore granice lewo i prawostronna co do pkt 3 tak? a jak wyjdzie + nieskonczonosc i −nieskonczonosc czyli dwie granice to co wtedy?

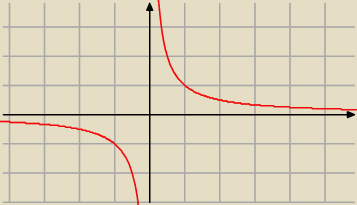
Ada: Nic, nie masz granicy w takim punkcie.

	1
np. funkcja f(x) =
	x

lim_x→0⁺ = +∞ lim_x→0⁻ = −∞ lim_x→0⁻≠lim_x→0⁺ ⇒ nie istnieje granica f(x) w x_o=0

mateusz: mhm oo super dzieki Ada duzy pluuus