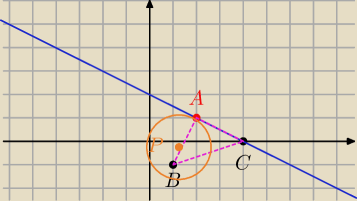
geo analityczna geometrykz: do sprawdzenia tok myślenia: W trójkącie równoramiennym ABC |AB|=|AC| dane są wierzchołki B=(1,−1), C=(4,0). Jedno z ramion trójkąta zawiera się w prostej x+2y−4=0. Na boku AB obrano taki punkt P że |AP| : |PB| = 3:2. Znajdź równanie okręgu o środku P i stycznego do boku AC

	1
A(x, −		x+2); trójkąt jest równoramienny, więc |AB|=|AC| ⇒
	2

	1		1
√(1−x)2+(−1+		x2}=√(4−x)2+(		x−2)2
	2		2

	18		10
z tego wyznaczyłem A(		,		), ale niestety, przy takich współrzędnych, odległości
	7		14

nie wychodzą takie same. co jest źle? popełniłem błąd rachunkowy(którego nie mogę się doszukać?!) czy w ogóle trzeba to zrobić jakoś inaczej?

Qulka:

Qulka: w pierwszym pierwiastku w drugim nawiasie powinno być chyba −3 (bo −1−2)

geometrykz: racja nie mogę się wyzbyć głupich błędów, na przykład dzisiaj na sprawdzianie zapomniałem spierwiastkować promienia i podstawiałem r² przy sprawdzaniu |r₁+r₂| no nic, dziękuję, teraz już sobie poradzę