Stereometria
que: Spośród wszystkich ostrosłupów prawidłowych czworokątnych o krawędzi bocznej a wybieramy ten,
dla którego przekrój płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy
oraz wierzchołek ostrosłupa ma największe pole. Znajdź objętość tego ostrosłupa
9 lut 22:25
que: hm?
9 lut 22:44
que: 
9 lut 23:07
que: pomoccy : (
10 lut 10:21
Eve:
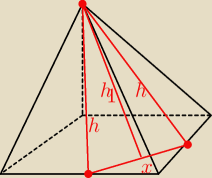
10 lut 10:41
Eve: | | 1 | |
kolizja oznaczeń, weź x= |
| b√2, b − krawędź podstawy |
| | 2 | |
10 lut 10:44
J:
zadanie niebanalne ... problem sprowadza się do wyznaczenia pola trójkąta (przekroju)
jako funkcji kata α ( kat nachylenia krawedzi do podstawy) ... algorytm:
1) wyznacz przekatna podstawy f(α)
2) wyznacz krawedź podstawy f(α)
3) wyznacz podstawe przekrouj f(α)
4) wyznacz wysokośc przekroju ( Tw. Pirtagorasa z wykorzystaniem wysokości ściany pocznej)
f(α)
5) wyznacz maksimum otrzymanej funkcji ( zaleąnej tylko od α)
10 lut 10:50
Eve: dana jest krawędź boczna a
10 lut 11:17
J:
i co ?
10 lut 11:31
Eve: pole tego przekroju mozna zapisać jako funkcję krawędzi podstawy
10 lut 11:36
que: próbuję i wciąż nie wychodzi
11 lut 12:15
J:
1) policz przekątną podstawy
11 lut 12:18
Eve:
| | 1 | | 1 | | 1 | |
PΔ= |
| x*h1, x= |
| b√2, h1=√(a2− |
| b2) |
| | 2 | | 2 | | 4 | |
11 lut 12:19
J:
Eve skad masz b ( krawędź podstawy) ?
11 lut 12:24
Eve: tak
11 lut 12:24
Eve: wszystko ładnie wychodzi, choć pochodna wygląda na skomplikowaną
11 lut 12:27
J:
pytam skąd ja masz, przecież b nie jest dane
11 lut 12:27
Eve: przecież pole ma być największe, więc z pochodnej ją policzę
11 lut 12:28
J:
Eve .. w treści zadania jest dana tylko krawędź boczna a c, więc pytam skąd masz b ?
11 lut 12:30
Eve: nie mam b, wyznaczę ją dla największego pola przekroju
| | 1 | | 1 | | 1 | |
PΔ= |
| * |
| b√2*√(a2− |
| b2) |
| | 2 | | 2 | | 4 | |
P
Δ'=0
można wyznaczyć b?
11 lut 12:32
J:
OK .. widzę teraz ...
11 lut 12:36
Eve: uff, bo się tyle naliczyłam
i jakby było źle to
11 lut 12:36
11 lut 13:22
Eve: a jakie masz pierwiastki pochodnej?
11 lut 13:29
que: mi wychodzi zły wynik, skąd wzięłaś wysokość h1?
11 lut 13:35
Eve:
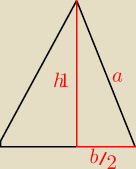
ze ściany bocznej
1
11 lut 13:39
11 lut 13:41
Eve:
| | √2 | | √2 | | 1*1/4*2b | |
P'= |
| √(a2−1/4b2)+ |
| b* |
| |
| | 4 | | 4 | | √a2−1/4b2 | |
11 lut 13:56
Eve:
| | 1 | | 1 | | 1 | |
a2− |
| b2>0, |
| |
| b<a, b<2a |
| | 4 | | 4 | | 2 | |
P'=0⇔..........=0 /*2
√a2−1/4b2
| | √2 | | 1 | | √2 | | 1 | | 4 | |
2 |
| (a2− |
| b2)− |
| b* |
| b=0 / * |
| |
| | 4 | | 4 | | 4 | | 2 | | √2 | |
w 2 składniku pochodnej ma być w liczniku − i w mianowniku 2, gdzieś mi umknęło
11 lut 14:15
Eve:
| | 2√3 | |
z tego wszystkiego V= |
| a3 |
| | 3 | |
11 lut 14:20
que: | | b√2 | |
czy tam zamaist b2 nie powinno byc |
| ? |
| | 4 | |
11 lut 21:26