Problem Wojtek: Udowodnij, że jeżeli środkowa trójkąta równa się połowie boku, do którego została poprowadzona, to trójkąt jest prostokątny.

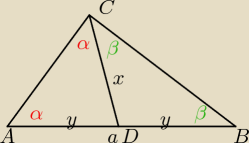
Nikka: x −środkowa trójkąta a − bok trójkąta, na który opuszczono środkową

	a		a
Z treści zadania x =		, środkowa dzieli bok a na połowy czyli y =		.
	2		2

Stąd wynika, że ΔACD i ΔBCD są równoramienne, a zatem |∡CAD| = |∡ACD| = α |∡BCD| = |∡CBD| = β Suma kątów w trójkącie wynosi 180^o |∡A| + |∡B| + |∡C| = 180^o α + β + (α+β) = 180^o 2α + 2β = 180^o α + β = 90^o czyli kąt przy wierzchołku C ΔABC ma miarę 90^o. ΔABC jest prostokątny.