Udowodnij kąty w czworokącie.
Ney:
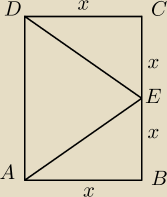
Dany jest czworokąt ABCD , w którym AB ∥ CD . Na boku BC wybrano taki punkt E , że |EC | = |CD
| i |EB | = |BA | . Wykaż, że kąt AED jest prosty.
Zrobiłem to tak :
Przy kącie EDC, CED zaznaczyłem α.
tak samo przy BEA, BAE również α.
Suma w trójkącie :
2α+90 stopni =180
2α=90
α=45
Kąt półprosty :
2α+ |kąt AED|=180
90 +|kąt AED|=180
|kąt AED|=90
Czy dobrze to zrobiłem? To zadanie maturalne.
9 lut 19:34
Ney: Refresh.
9 lut 20:30
Mila:
1) Rozważyłeś czworokąt, który jest prostokątem.
Dlaczego rozważyłeś przypadek, że CE=EB?
Z tw. odwrotnego do tw. Pitagorasa w ΔAED jest to prawda ,że kąt E jest prosty.
Trzeba rozwiązać w przypadku ogólnym.
2) Kąt półprosty? Chyba półpełny.
Podpowiadam
1) patrz na rysunek
2) wykorzystaj kąty w trapezie, kąty naprzemianległe, sumę kątów w ΔABE
3) wykaż, że α+γ=90
o
9 lut 20:41
Ney: Tak półpełny, błąd w pisaniu.
A skoro nie było wzmianki o tym, jaka jest zależność pomiędzy CE i EB to nie mogę przyjąć, że
są równe? Jak mam wiedzieć to jaka jest pomiędzy nimi zależnośc?
9 lut 20:58
Mila:
Jeżeli nie pisze, że są równe, to zakładasz, że mogą być różne.
Spróbuj dokończyć, to już jest łatwe.
9 lut 21:08
Mila:
9 lut 22:25
Ney: Już dokańczam
9 lut 22:26
Mila:
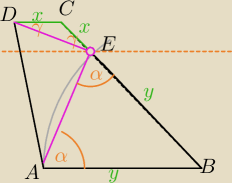
∡AED=α+γ ( masz tam kąty naprzemianległe wewnętrzne ,
prosta przechodząca przez E jest równoległa do AB i DC)
∡ABE=2γ
2γ+2α=180 w ΔABE⇔
α+γ=90o.
============
9 lut 22:32
Ney: Zroobione. Mila dzięki wielkie, świetnie można się od Ciebie nauczyć
9 lut 22:34
Mila:
9 lut 22:36
 Dany jest czworokąt ABCD , w którym AB ∥ CD . Na boku BC wybrano taki punkt E , że |EC | = |CD
| i |EB | = |BA | . Wykaż, że kąt AED jest prosty.
Zrobiłem to tak :
Przy kącie EDC, CED zaznaczyłem α.
tak samo przy BEA, BAE również α.
Suma w trójkącie :
2α+90 stopni =180
2α=90
α=45
Kąt półprosty :
2α+ |kąt AED|=180
90 +|kąt AED|=180
|kąt AED|=90
Czy dobrze to zrobiłem? To zadanie maturalne.
Dany jest czworokąt ABCD , w którym AB ∥ CD . Na boku BC wybrano taki punkt E , że |EC | = |CD
| i |EB | = |BA | . Wykaż, że kąt AED jest prosty.
Zrobiłem to tak :
Przy kącie EDC, CED zaznaczyłem α.
tak samo przy BEA, BAE również α.
Suma w trójkącie :
2α+90 stopni =180
2α=90
α=45
Kąt półprosty :
2α+ |kąt AED|=180
90 +|kąt AED|=180
|kąt AED|=90
Czy dobrze to zrobiłem? To zadanie maturalne.
 1) Rozważyłeś czworokąt, który jest prostokątem.
Dlaczego rozważyłeś przypadek, że CE=EB?
Z tw. odwrotnego do tw. Pitagorasa w ΔAED jest to prawda ,że kąt E jest prosty.
Trzeba rozwiązać w przypadku ogólnym.
2) Kąt półprosty? Chyba półpełny.
Podpowiadam
1) patrz na rysunek
2) wykorzystaj kąty w trapezie, kąty naprzemianległe, sumę kątów w ΔABE
3) wykaż, że α+γ=90o
1) Rozważyłeś czworokąt, który jest prostokątem.
Dlaczego rozważyłeś przypadek, że CE=EB?
Z tw. odwrotnego do tw. Pitagorasa w ΔAED jest to prawda ,że kąt E jest prosty.
Trzeba rozwiązać w przypadku ogólnym.
2) Kąt półprosty? Chyba półpełny.
Podpowiadam
1) patrz na rysunek
2) wykorzystaj kąty w trapezie, kąty naprzemianległe, sumę kątów w ΔABE
3) wykaż, że α+γ=90o