stereometria Marta: graniastoslup prawidlowy czworokatny o wysokosci 4 razy krotszej od krawędzi podstawy przecięto płaszczyzną przechodzącą przez przekątną dolnej podstawy i środki dwóch sąsiednich krawędzi górnej podstawy. Pole otrzymanego przekroju jest równe 36. Oblicz pole podstawy graniastosłupa. Nie wiem jak wyznaczyć h w trapezie.

Kacper: Z twierdzenia Pitagorasa

Marta: no tak, ale, nie rozumiem tego, powinno być h²=(a/4)²+(a√2/4)² ale nie rozumiem skąd bierze sie a√2/4 a to długość boku podstawy

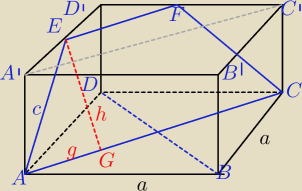
Mila: |AC|=|A'C'|=a√2

	1
|EF|=		a√2
	2

	1		a√2
g=(a√2−		a√2):2=
	2		4

W ΔAA'E:

	a		a
c2=(		)2+(		)2
	4		2

	5a2
c2=
	16

W ΔAGE:

	5a2		a√2
c2=|AG|2+h2⇔		=(		)2+h2
	16		4

oblicz h=...

a√2+a√22
	*h=36⇔po przekształceniach:
2

a*h=24√2 dokończ

Mila: Taki alarm i żadnego zainteresowania rozwiązaniem.

Eta: Dziękuję bardzo Mila