stożek wpisany w kulę
alexia: W kulę o promieniu R wpisano stożek obrotowy. Dla jakiego promienia r podstawy stożka jego
objętość będzie największa ?
9 lut 14:22
Eve:
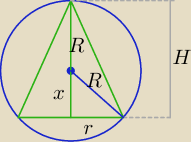
9 lut 14:45
alice: Tyle wiem

Czuję, że w pierwszym kroku trzeba zauważyć jakąś zależność, której ja niestety
nie widzę

9 lut 14:49
alice: Podpowiedz czy coś da skorzystanie z tego , że r2 + x2 = R2 ?
9 lut 14:50
Eve:
H=R+x, a x ze słynnego Nazwiska policz

9 lut 14:51
J:
| | 1 | | 1 | |
V = |
| πr2*H = |
| π(R2 − x2)(R + x) i badasz ekstrmum |
| | 3 | | 3 | |
9 lut 14:51
alice: jak zbadać ekstremum skoro mam 2 niewiadome?
9 lut 14:54
J:
a która druga ?
9 lut 14:55
alice: R i x
9 lut 14:57
J:
R jest dane, przeczytaj treść zadania

9 lut 14:59
alice: No tak

Do tej pory robiłam tylko zadania gdzie wychodziło np: V =
√34 (6a
2 − 2a
3).
I z tym umiałam sobie poradzić a z tym mimo Waszej pomocy nie mogę sobie dać rady.
9 lut 15:02
J:
tutaj traktujesz R jako stałą
| | 1 | |
V = |
| π(R3 + R2x −Rx2 −x3) ... i teraz liczysz pochodną |
| | 3 | |
9 lut 15:04
alice: V' = 13 π (R2 −2Rx − 3x2 )?
9 lut 15:08
J:

9 lut 15:09
alice: domyślam się , że powinnam teraz sprawdzić kiedy V' = 0, ale tu znów jestem bezsilna

9 lut 15:11
J:
to trójmian kwadratowy ... oblicz Δ oraz x1 i x2
9 lut 15:12
alice:
nawiasu:
Δ = 16R2
√Δ = 4R
x1 = −R
x2 = 1/3 R
9 lut 15:15
J:
| | 1 | |
x1 odpada ( bo ujemne ) , zatem x = |
| R i jest to maksimum, bo pochodna zmienia znak z |
| | 3 | |
dodatniego na ujemny .. .teraz policz r i koniec zadania
9 lut 15:18
alice: r =
√R2 − x2
czyli r =
2√23 R . wszystko się zgadza. Dzięki piękne

9 lut 15:26

 Czuję, że w pierwszym kroku trzeba zauważyć jakąś zależność, której ja niestety
nie widzę
Czuję, że w pierwszym kroku trzeba zauważyć jakąś zależność, której ja niestety
nie widzę


 Do tej pory robiłam tylko zadania gdzie wychodziło np: V = √34 (6a2 − 2a3).
I z tym umiałam sobie poradzić a z tym mimo Waszej pomocy nie mogę sobie dać rady.
Do tej pory robiłam tylko zadania gdzie wychodziło np: V = √34 (6a2 − 2a3).
I z tym umiałam sobie poradzić a z tym mimo Waszej pomocy nie mogę sobie dać rady.


