 Pole podstawy:
Pole podstawy:
| 62√3 | 36√3 | |||
Pp=6* | =6* | =54√3 | ||
| 4 | 4 |
| 6√3 | ||
r= | =3√3 | |
| 2 |
| 1 | ||
V= | *54√3*9=162√3 | |
| 3 |
 Ponieważ podstawą jest sześciokąt foremny, to składa się on z 6 trójkątów równobocznych, czyli:
Pp=6*(a2√3/ 4)=54√3
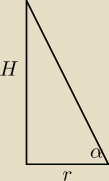
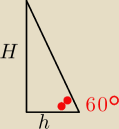
Ściana boczna jest nachylona pod kątem 60o, czyli można ,,wyciągnąć" trójkąt (rysunek):
H − wysokość ostrosłupa
h − wysokość jednego z trójkątów z podstawy
h=a2√3/2=3√3
tg60o=√3⇒√3=Hh⇒√3=H3√3⇒H=9
V=13*54√3*9=162√3
Ponieważ podstawą jest sześciokąt foremny, to składa się on z 6 trójkątów równobocznych, czyli:
Pp=6*(a2√3/ 4)=54√3
Ściana boczna jest nachylona pod kątem 60o, czyli można ,,wyciągnąć" trójkąt (rysunek):
H − wysokość ostrosłupa
h − wysokość jednego z trójkątów z podstawy
h=a2√3/2=3√3
tg60o=√3⇒√3=Hh⇒√3=H3√3⇒H=9
V=13*54√3*9=162√3
