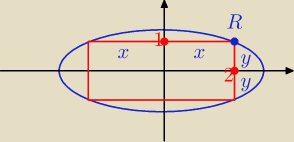
proszę o szybką pomoc!!! ada: Prostokąt wpisany w elipsę o równaniu x2/4+y2=1 mają boki równoległe do osi układu współrzędnych.Jakie są wymiary prostokąta o największym polu ?

Janek191:

x2
	+ y2 = 1 ⇒ y2 = 1 − 0,25 x2 ⇒ y = √ 1 − 0,25 x2
4

x2		y2
	+		= 1
22		12

a = 2 , b = 1 Pole prostokąta R = ( x; y) 0 < x < 2 i 0 < y < 1 P = 2 x* 2 y = 4 x y = 4 x*√ 1 − 0,25 x² = x*√16 − 4 x² więc P( x) = x*√16 − 4 x² Pochodna

	− 8 x
P'(x) = √16 − 4 x2 + x*		=
	2√16 − 4 x2

	16 − 4 x2		4 x2		16 − 8 x2
=		−		=		= 0 ⇔
	√16 − 4 x2		√ 16 − 4 x2		√16 − 4 x2

⇔ 16 − 8 x² = 0 ⇔ 2 = x² ⇔ x = √2 W punkcie x = √2 funkcja P' zmienia znak z + na − , czyli mamy maksimum funkcji P. Wtedy pole prostokąta jest równe: P ( √2) = √2*√16 − 4*(√2)² = √2*√8 = √16 = 4 P_max = 4 ===========

Janek191: Wymiary prostokąta o największym polu: x = √2 więc

	1
y = √ 1 − 0,25*(√2)2 = √ 1 − 0,5 = √0,5 =		= 0,5 √2
	√2

Wymiary prostokąta: 2 x = 2*√2 2 y = 2*0,5√2 = √2 Odp. 2√2 , √2 ================