uklady rownan - metoda wyznacznikow Lenka: Dla jakich wartosci parametru m rozwiazaniem ukladu rownan x+my=1 2x−y=m jest para spelniajaca nierownosc |x−y|≤1 ? mam to zrobic metoda wyznacznikow no i narazie mam W=−1−2m Wx=−1−m² Wy=m−2 ^Wx_W=^−(m2+1)_−(2m+1)=^{(m+1)(m+1)−2m}_2m+1 ^Wy_W=^m−2_−(m²+1) no i dalej juz nie wiem jak mam to zrobic dlatego prosze o pomoc

Qulka:

	Wy		m−2
y=		=
	W		−1−2m

potem wstawiasz do równania z modułem zamiast x i y i liczysz m

Lenka: ^Wy_W=^m−2_−1−2m sorki za blad

Lenka: no a to Wx mam dalej liczyc czy tez juz wstawiac do rownania?

Qulka: wstawić w takiej postaci jak miałaś na początku

Lenka: a okej

Lenka: no i mam teraz ^{−1−m2+m−2}_−1−2m=^{−(m2−m+1+2}_−(2m+1)=^m2−m+1+2_2m+1=^{(m+1)(m−1)−m+2}_2m+1 no i co dalej

Qulka: miałaś x−y wiec −m+2

Qulka: używaj dużej literki U do ułamków

Lenka: no tak no to wtedy wychodzi

m2+m−1
1+2m

Lenka: moze jakas wskazowka?

Qulka: no i teraz dwie nierówności czyli pozbywasz się modułu to ≤1 i to≥−1

Lenka: bo jak znam zycie to pewnie mozna w jakis chytry sposob rozpisac tylko nie mam pojecia w jaki teraz mam juz tak ale co dalej to juz sama nwm

m(m+1)−1
1+2m

Qulka: i jedynkę na drugą stronę i do wspólnego mianownika

Lenka: i mam pomnozyc jedynke przez to co jest pod ulamkiem?

Qulka: jak sprowadzasz do wspólnego tak

Lenka: no mam teraz w pierwszej opcji

m2+m−1		1+2m		m2−m−2
	−		=		≤0
1+2m		1+2m		1+2m

Qulka: tak i teraz mnożymy przez kwadrat mianownika żeby nie zmienić znaku nierówności

Qulka: a z górnego liczymy deltę i miejsca zerowe

Lenka: czyli m₁=−1 m₂=2

Lenka: a z drugiego m₁=−3 m₂=0

Lenka: i to wszystko?

Qulka: czyli mamy (m+1)(m−2)(1+2m)≤0 i rysujemy siatkę znaków (czyli wężyk zwany falką )

Lenka: skad to wziales?

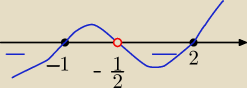
Qulka: czyli z pierwszego m∊(−∞;−1> u (−1/2 ; 2>

Lenka: skad sie wzielo (m+1)(m−2)(1+2m)≤0 bo nie rozumiem

Lenka: dlaczego to jest pomnozene i mniejsze od 0

Qulka: jak pomnożyłaś przez kwadrat mianownika to jeden się skrócił drugi został jako ostatni nawias a pierwsze dwa nawiasy to z delty z licznika

Lenka: to znaczy ja myslalam wczesniej ze odpowiedzia jest to co z delty wyliczylam... to po co delte liczyc skoro to sie wzielo z poprzedniego kroku?

Lenka: to chyba delte w takim razie mozna bylo pominac czy zle mysle?

Qulka: po to liczyłaś deltę żeby mieć te wartości "m" co są na osi (co ja zapisałam w postaci nawiasów) ale używając Twoich wyliczeń

Lenka: ahaa to juz rozumiem

Qulka: trzecia wartość to z mianownika

Lenka: czyli do tego drugiego to bedzie wyglac tak (m²+3m)(1+2m)≥0

Qulka: tak

Lenka: jak mozna m²+3m rozpisac?

Lenka: wiem m(m+3)(1+2m)≥0

Qulka: albo z delty albo po prostu m przed nawias m(m+3) m=0 lub m=−3

Qulka: tak

Lenka:

	1
kolejno −3 −		0
	2

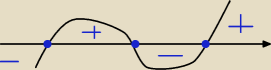
Lenka:

	1
czemu orzy −		u cb jest kolko puste?
	2

Lenka: przy*

Lenka:

	1
jesli to kolko u mnie tez jest puste to bedzie m∊<−3,−		)∪<0,+∞)
	2

Lenka: dlaczego to kolko jest puste? teraz mam zrobic suma czy czesc wspolna tych 2 opcji z m∊... ?

Lenka: obstawiam ze suma

Qulka: też puste, bo jest z mianownika, a mianownik nie może być równy zero tu część wspólna tych dwóch

Qulka: bo było | | ≤ a więc środek

Lenka: no tak czyli ostateczny wynik to <−3,−1>∪<0,2>

Qulka: tak

Lenka: okej dzieki za pomoc i czas ktory dla mnie poswiecilas Qulka bo gdyby nie ty w ogole bym z tym nie ruszyla

Lenka: tak na marginesie fajnie tlumaczysz