rysunek funkcji abc: jak narysowac funkcje 2xe^x2? hmmm

Arlan: najlepiej zbadać najpierw przebieg jej zmienności

Qulka: http://www.wolframalpha.com/input/?i=2xe%5Ex%5E2

abc: ok dzieki. a teraz jezeli mialbym obliczyc pole obszaru ograniczonego liniami wlasnie ta funkcja na gorze oraz x=1 oraz x=−1 oraz osia OX. jak to policzyc?

Qulka: całka od −1 do 1 z tej funkcji a w tym przypadku od 0 do 1 i wynik razy dwa (bo jak jest pod osią to pole się odejmuje)

Qulka: http://www.wolframalpha.com/input/?i=2xe%5Ex%5E2+from+-1+to+1 policzył bestyja

abc: chodzi o minus przed calke tak? w tym przypadku dwie takie same figury i dlatego razy 2? po prostu liczyc calke od 0 do 1 z powyzszej funkcji?

Qulka: tak

abc: dziekuje bardzo Quleczko

abc: jestes moze jeszcze?

Qulka: jestem

abc: chcialem zapytac ile powinno wyjsc finalnie

abc: nie za pozna pora ?

Qulka: powinno wyjść 2e, a wolfram policzył długość linii, a nie pole

abc: a nie 2−2e hmmm ? wlasnie cos mi sie zdawalo troche oszukal ten wolfram

abc: e^x2 dlq 0 bd 1 a dla 1 bedzie e. 2(1−e)=2−2e ?

Qulka: jak już to 2e−2 bo od końca odejmujesz początek i tak jak mówiłam wychodzi mu 0 bo odejmuje to co pod spodem http://www.wolframalpha.com/input/?i=integral++2xe%5Ex%5E2+from+-1+to+1 a od 0 liczy ładnie integral 2xe^x2 from 0 to 1

Qulka: http://www.wolframalpha.com/input/?i=integral++2xe%5Ex%5E2+from+0+to+1

abc: obliczyc pole obszaru ograniczonego x²−x−6 oraz −x²+5x+14

abc: przecinaja sie w −2 (parabole). a teraz zeby znalezc drugie miejsce zerowe to wziac te funkcje w uklad i pozniej normalnie calka? tylko z jakiej funkcji?

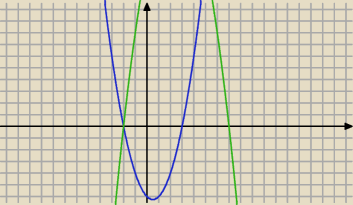
Qulka: całka od −2 do 5 z (−x²+5x+14 − (x²−x−6))

Qulka: od górnej funkcji odejmujesz dolną

Qulka: http://www.wolframalpha.com/input/?i=integral+%28-x%5E2%2B5x%2B14+-+%28x%5E2-x-6%29%29++from+-2+to+5

abc: dziekuje za pomoc. dobranoc