xx Pomocy: a jaka jest monotoniczność tej funkcji?

	1
1−
	(x−1)2

czy to bd f(x) malejący dla (−∞,0) (2,0) rosnąca dla (0,1)(1,2)

Eve: a obliczyłeś to?

Pomocy: No to jest pochodna, przyrównałam do zera, bo dziedzina jest z wyłączeniem 1 i teraz nie wiem czy oby na pewno będzie będzie taka monotoniczność

Eve: to co napisałes to juz jest pochodna?

Pomocy: Tak

Eve:

x2−2x+1−1
	>0
(x−1)2

x²−2x>0 to liczyłeś?

Pomocy: Nie, zrobiłam wykres, bo miejsca zerowe to 2 i 0, potem wyznaczyłam monotoniczność z wyłączeniem 1 A nie wiem skąd się wzięło to co Ty napisałeś/aś

Eve: ja sprowadziłam do wspólnego mianownika, jak inaczej?

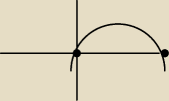
Pomocy: Punkty to 0 i 2 i z tego wyznaczyłam monotoniczność z wyłączeniem 1

Pomocy: Ok, wychodzi na to że chyba mam dobrze

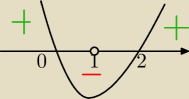
Eve: tylko, że ja mam

Pomocy: No tak ale z tego x²−2x>0 x(x−2)>0 x>0 x>2 i to jest rosnąca, jeśli teraz postawisz, −1 >0 to bd, błąd ja to tak rozumiem

Pomocy: Ale wiem, że twój wykres jest dobry, dlatego mam dylemat jak to powinno być

Eve: rosnąca, dla (−∞,0)∪(2,0) malejaca dla (0,1)∪(1,2)

Pomocy: Ok, czyli mam odwrotnie, dzięki

Eve: bo odwrotnie parabole masz

b.:

	1
poprawka: 1−		jest malejąca na (−∞,1) i rosnąca na (1,∞)
	(x−1)2