#a:
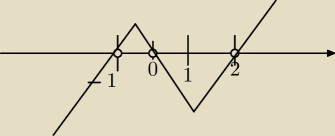
f(x)= x
2−6x+6ln(x+1)
f'(x)= (x
2)'−(6x)'+(6ln(x+1))'
| | 1 | |
f'(x)= 2x−6+6* |
| *(x+1)'+0*ln(x+1) |
| | x+1 | |
Monotonicznośc
f'(x)>0
2x(x+1)
2−6(x+1)
2+6(x+1)>0
2x(x
2+2x+1)−6(x
2+2x+1)+6(x+1)>0
2x
3+4x
2+2x−6x
2−12x−6+6x+6>0
2x
3−2x
2−4x>0
x
3−x
2−2x>0
x(x
2−x−2)>0
x(x+1)(x−2)>0 dla x∊(−1,0) U(2,
∞)
f'(x)<0 dla x∊(−
∞,−1) U (0 ,2)
Ekstrema
2x
2−4x=0
x
2−2x=0
x(x−2)=0 x=0 i x=2
Teraz zbadac znak pochodnej wokól rozwiązan
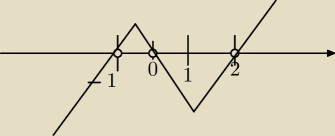 f(x)= x2−6x+6ln(x+1)
f'(x)= (x2)'−(6x)'+(6ln(x+1))'
f(x)= x2−6x+6ln(x+1)
f'(x)= (x2)'−(6x)'+(6ln(x+1))'