geo analityczna.. znowu.
geometrykz: napisz równanie okręgu przechodzącego przez punkt M=(0,1) i stycznego do dwóch prostych o
równaniach x+y−2=0 i x+y+3=0
zauważam na początku, że proste są rownoległe, więc wyznaczam prostą prostopadłą do nich,
przechodzącą przez punkt M. Liczę punkty wspólne i wyznaczam A i B(punkty przecięcia
prostopadłej z równoległymi). Liczę odległość |AB| i ona ma równać się 2r(dwa razy długość
promienia), a dodatkowo środek okręgu to współrzędne środka odcinka AB. Otrzymuję prawidłowe
równanie, z tym, że w odpowiedzi są dwa przypadki. Jak wyznaczyć drugi przypadek?
7 lut 17:53
Eve:
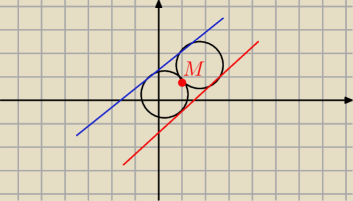
7 lut 18:09
geometrykz: no tak, ależ gafa! ja durny przyjąłem, że M to środek okręgu, a przecież jasno jest napisane,
że okręgi przechodzą przez ten punkt.
dziękuję Eve, teraz sobie już poradzę

7 lut 18:12
Eve: nie zrobiłeś rysunku?


7 lut 18:13
Eve: i jak mogłeś założyć, że okrąg przechodzi przez swój środek

7 lut 18:14
geometrykz: zrobiłem rysunek: oś rzędnych, odciętych, punkt M, dwie proste rownoległe, prosta przechodząca
przez M i środek odcinka AB, bo nie wczytałem się w treść, chcąc szybciej zrobić zadanie i
wszystko wyszło błędnie, przez co zamiast zrobić szybciej, to wyjdzie mi dwa razy dłużej.
Cóż..

7 lut 18:16
geometrykz: no właśnie

totalnie niezrozumienie z mojej strony

7 lut 18:17
Mila:
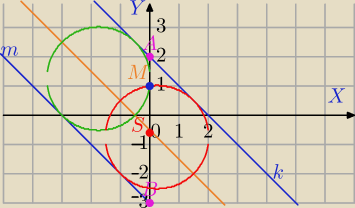
1) Rysuję proste w układzie wsp.
k: x+y−2=0 i prosta m: x+y+3=0
k: y=−x+2 i
m: y=−x−3
2) k||m⇒środek okręgu stycznego do prostych leży na prostej równoległej do k i m przechodzącej
przez środek odcinka AB
| | 2+(−3) | | 1 | |
S=(0, |
| )=(0,− |
| ) |
| | 2 | | 2 | |
| | 1 | |
So=(a,−a− |
| ) środek okręgu |
| | 2 | |
3) promień okręgu:
| | | | 2.5 | | 2.5√2 | |
d(S,k)= |
| = |
| = |
| =r |
| | √1+1 | | √2 | | 2 | |
⇔
| | 6,25 | |
(x−a)2+(y+a+0,5)2= |
| |
| | 2 | |
okrąg przechodzi przez punkt M=(0,1)⇔
| | 6,25 | |
(0−a)2+(1+a+0,5)2= |
| ⇔ |
| | 2 | |
dokończ , otrzymasz dwa rozwiązania.
7 lut 20:50
Eta:
Dziękuję bardzo
Mila 
7 lut 23:26
Mila:

7 lut 23:34
Eta:

7 lut 23:35
geometrykz: ojej, kurczę, nawet nie widziałem jak ktoś się dla mnie natrudził

dziękuję Mila, ale zadanie
już dawno zrobiłem. może ktoś kiedyś je wygoogluje i trafi właśnie na tę stronę

7 lut 23:38
Mila:
7 lut 23:39
geometrykz: zrobiłbym jakiś ładny rysunek w podzięce, ale nie umiem, a na razie nie mam czasu na naukę
rysowania. Kiedyś się może nauczę

7 lut 23:41
Eta:

7 lut 23:43






 totalnie niezrozumienie z mojej strony
totalnie niezrozumienie z mojej strony 
 1) Rysuję proste w układzie wsp.
k: x+y−2=0 i prosta m: x+y+3=0
k: y=−x+2 i
m: y=−x−3
2) k||m⇒środek okręgu stycznego do prostych leży na prostej równoległej do k i m przechodzącej
przez środek odcinka AB
1) Rysuję proste w układzie wsp.
k: x+y−2=0 i prosta m: x+y+3=0
k: y=−x+2 i
m: y=−x−3
2) k||m⇒środek okręgu stycznego do prostych leży na prostej równoległej do k i m przechodzącej
przez środek odcinka AB



 dziękuję Mila, ale zadanie
już dawno zrobiłem. może ktoś kiedyś je wygoogluje i trafi właśnie na tę stronę
dziękuję Mila, ale zadanie
już dawno zrobiłem. może ktoś kiedyś je wygoogluje i trafi właśnie na tę stronę 

